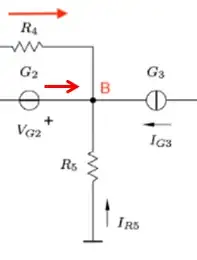
I am trying to analyze the circuit given below:
The reference node is in the bottom with 0 V.
At nodes A and B writing down Kirchhoff’s first law equation trying to express each current in terms of the voltage across the branch.
My equation for node A looks like this:
$$ \frac{V_{G_1}-V_A}{R_1} - \frac{V_A-V_{reference}}{R_2} - \frac{V_A-V_{reference}}{R_3} + \frac{V_A-V_B}{R_4} + I_{G_2} = 0 $$
For node B:
$$ -I_{G_3} - \frac{V_B-V_{reference}}{R_5} - \frac{V_B-V_A}{R_4} + I_{G_2} = 0 $$
As of now I only have two equations and three unknowns. Therefore I am not sure if my solution attempt is correct.