0

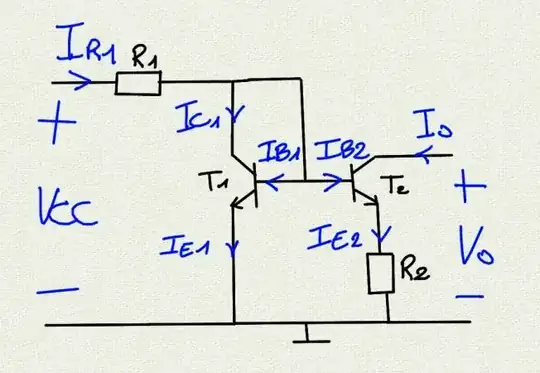from the Widlar schema enter image description here that you can see, from here, i don't know how to retrieve this formula : $$ I_{C1} = {\beta_1 \over {\beta_1+1}} \left( I_{R1} - {I_{C2} \over \beta_2} \right) $$

user7058377
  • 99
  • 6
  • 1
    The formulas mean little when there's no **schematic** to relate them to. Sure, I can follow the link and look there but I'm too lazy so include it here. And what is your actual question? – Bimpelrekkie Sep 15 '20 at 10:59
  • What can't you retrieve? – Andy aka Sep 15 '20 at 11:05
  • your first formula differs from that in the article you link to. – RJR Sep 15 '20 at 11:38
  • I don't know how to retrieve is this formula (corrected) : $$ I_{C1} = {\beta_1 \over {\beta_1+1}} \left( I_{R1} - {I_{C2} \over \beta_2} \right) $$. I put the schema too... – user7058377 Sep 15 '20 at 12:40

2 Answers2

2

Ok , I get the solution :

With these formulas : enter image description here

from enter image description here

and KCL in A and after in B :

$$ I_{R1} = I_{C1} + (I) $$ $$ I_{R1} = I_{C1} + (I_{B1}+I_{B2}) $$

i get

enter image description here

user7058377
  • 99
  • 6
  • Please accept your own answer (by clicking the tick button right under the points) so that the question does not remain open. – Rohat Kılıç Sep 15 '20 at 14:13
0

Notice that a \$Q_1\$ is a diode-connected BJT thus, without \$Q_2\$ we see that:

\$I_{R1} = I_{B1} + I_{C1} = I_{E1}\$

And now if we add \$Q_2\$ we have:

\$I_{R1} = I_{E1} +I_{B2} =I_{E1} +\frac{I_{C2}}{\beta2}\$

but you want to know the \$Q_1\$ collector current:

\$I_{E1} = I_{R1} - I_{B2}\$

\$I_{C1} = \alpha*I_{E1}\$

\$I_{C1} = (I_{R1} - I_{B2})*\alpha\$

Additional we know that

\$\frac{I_C}{I_E} = \alpha = \frac{I_B *\beta }{I_B*\beta + I_B} = \frac{\beta}{\beta +1} \$

therefore

\$I_{C1} = \alpha \left(I_{R1} - I_{B2}\right) = \frac{\beta}{\beta +1}\left(I_{R1} -\frac{I_{C2}} {\beta2}\right)\$

G36
  • 13,642
  • 1
  • 18
  • 33