Simplify the boolean function $$Z=A\bar B \bar{C_i} + \bar A B \bar{C_i} + \bar A\bar B {C_i} + A B {C_i}$$

Question

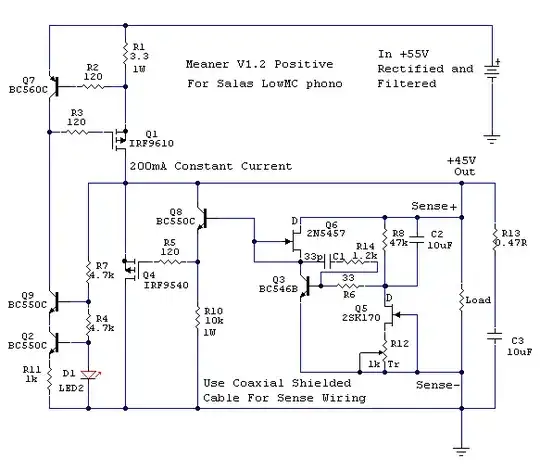
I want to simplify the following boolean function:

$$Z=A\bar B \bar{C_i} + \bar A B \bar{C_i} + \bar A\bar B {C_i} + A B {C_i}$$

Here's my attempt:

\begin{align} Z &= A\bar B \bar{C_i} + \bar A B \bar{C_i} + \bar A\bar B {C_i} + A B {C_i} \\ & = \bar{C_i}(A \bar B + \bar A B) + C_i(\bar A \bar B + AB) \\ & = \bar C_i(A \oplus B) + C_i(A \equiv B) \end{align}

I thought this was the end of it but in my textbook it continues and has: \begin{align} Z &= A\bar B \bar{C_i} + \bar A B \bar{C_i} + \bar A\bar B {C_i} + A B {C_i} \\ & = \bar{C_i}(A \bar B + \bar A B) + C_i(\bar A \bar B + AB) \\ & = \bar C_i(A \oplus B) + C_i(A \equiv B) \\ & = A \oplus B \oplus C_i \\ & = A \equiv B \equiv C_i \end{align}

I'm confused about what happened between the third and fourth step. What boolean algebra rules are being used here?

$$A \equiv B$$ is the same as NOT $${(A \oplus B)}$$ (sorry not very good at formulas) — jcaron, Sep 02 '20 at 21:05
@jcaron Yes but I'm trying to figure out why $$\bar C_i(A \oplus B) + C_i(A \equiv B)=A \oplus B \oplus C_i$$. — Ski Mask, Sep 03 '20 at 12:02
It's another instance of (X AND NOT Y) OR (NOT X AND Y) = X XOR Y, with X being Ci here and Y being A XOR B. — jcaron, Sep 03 '20 at 12:07
By \$X\equiv Y \$, what do you mean exactly? I've never seen this notation so far. — edmz, Sep 04 '20 at 19:10
Seems like $$A\equiv B$$ is the same as $$\overline{(A\oplus B)}$$. In that case, $$\begin{align} Z&=\overline{C_i} (A \oplus B) + C_i (A\equiv B)\\ &=\overline{C_i} (A \oplus B) + C_i\overline{(A \oplus B)} \\ &= C_i \oplus (A\oplus B)\\ &=A\oplus B\oplus C_i \end{align}$$ — cjferes, Sep 04 '20 at 21:50
Are there any solver tools that can brute-force (or use other heuristics to obtain) a solution to this sort of problem? — Sean, Sep 05 '20 at 22:04
@Sean Unfortunately this is from a written question from a past paper. So I have to show all my working out and the laws that I used. — Ski Mask, Sep 07 '20 at 11:19
@Ski Mask, I was actually asking out of my own interest, and I'm still interested in the answer! — Sean, Sep 07 '20 at 17:57
Brute force would be cool. I wonder if some optimization algorithm could be found for minimizing the number of operators used. Some kind of derivative for this problem? Perhaps AI? — sergiu reznicencu, Sep 07 '20 at 18:49
Or better. Just assume the final result contains all inputs used once with one operator in between. This is very much possible — sergiu reznicencu, Sep 07 '20 at 18:51

score 5 · Answer 1 · edited Sep 05 '20 at 16:10

5

Observe that
\begin{align}\overline{\overline{A} \cdot\overline{B} + A\cdot B} = \overline{(\overline{A}\cdot\overline{B})}\cdot\overline{(A \cdot B)} = (A + B)\cdot(\overline{A}+\overline{B}) = A \cdot\overline{B} + \overline{A}\cdot B \end{align}

Hence

\begin{align} Z&=\overline{C_i} (A \oplus B) + C_i (A\equiv B)\\ &=\overline{C_i} (A \oplus B) + C_i\overline{(A \oplus B)} \\ &= C_i \oplus (A\oplus B)\\ &=A\oplus B\oplus C_i \end{align}

edited Sep 05 '20 at 16:10

answered Sep 05 '20 at 13:49

Shashank V M

2,279
13
47

1

Ah I see. I made the mistake of taking $$A \equiv B = A \oplus B$$ and not $$\lnot{(A \oplus B)}$$ – Ski Mask Sep 07 '20 at 11:18

score 4 · Accepted Answer · answered Sep 07 '20 at 23:22

When in doubt about booleans, just build a truth table.

Truth tables for XOR (\$\oplus\$):

   | 0 | 1
---+---+---
 0 | 0 | 1
---+---+---
 1 | 1 | 0

For "is equal to" (\$\equiv\$):

   | 0 | 1
---+---+---
 0 | 1 | 0
---+---+---
 1 | 0 | 1

As you can see \$A \equiv B\$ gives just the opposite result of \$A \oplus B\$ (the result is 1 for the first when it is 0 for the second, and vice-versa). This means that:

$$A \equiv B = \overline{A \oplus B}$$

You used several times the identity $$X\overline{Y} + \overline{X}Y = X \oplus Y$$

This means: If (X is true AND Y is false) OR (if X is false and Y is true) is the same as either X or Y is true, but not both, which is quite straightforward.

So now you get to this equation:

$$\overline{C_i}(A \oplus B) + C_i(A \equiv B) \\$$

Since \$A \equiv B\$ can be written as \$\overline{A \oplus B}\$, you can rewrite it to:

$$\overline{C_i}(A \oplus B) + C_i(\overline{A \oplus B}) \\$$

Which is a form of \$X\overline{Y} + \overline{X}Y\$, with \$X = C_i\$ and \$Y = A \oplus B\$.

So it can then be rewritten to:

$$C_i \oplus (A \oplus B)$$

As all these boolean operators are commutative, this be be rewritten as:

$$A \oplus B \oplus C_i$$

schnedan · Answer 3 · 2020-09-07T12:51:02.483

0

First, plus is an unusual operator for bool equations Wikipedia. I assumed you referencing a OR

With this assumtion I came to the result: no further reduction possible. For This I used a Karnaugh map

https://en.wikipedia.org/wiki/Karnaugh_map

edited Sep 07 '20 at 12:51

answered Sep 07 '20 at 10:15

schnedan

2,538
7
16

1

[Leibniz used + for inclusive OR](https://www.hf.uio.no/ifikk/forskning/publikasjoner/tidsskrifter/njpl/vol2no1/history.pdf) and Boole used it too, so it's been around for over 300 years. Nowadays, it's more usual to use + for OR and ⊕ for XOR because it's far more readable. See discussion [here](https://electronics.stackexchange.com/questions/131317/why-is-the-sign-commonly-used-as-logic-or-operator). Plus, there's far more to reduction than Karnaugh Maps, e.g. De Morgan's Laws. Don't believe everything you read on Wikipedia. – tim Sep 07 '20 at 12:30
I only quote wikipedia if it states things I know to be correct an are also in my books... I work in electronics for 25 years now, and never saw a plus for OR from any professional... – schnedan Sep 07 '20 at 12:38
also as you can see in the formula als well as in the Karnaugh_map there are always 2 of 3 elements different in any case and there is no 2 Element term which can be reused without modification (like invert) in an other therm. So if there is a further reduction I like to learn how, but I don't see any – schnedan Sep 07 '20 at 12:47
Things like De Morgan's Laws, to my knowledge are good for 5 or more variables where Karnaugh_maps start to be of no use. But if you can apply a simple scheme like Karnaugh_map its a valid measure to do so. – schnedan Sep 07 '20 at 12:54
As you can see, a 4-input OR gate with 3 NOT gates had been reduced to a 3-input XOR gate. The + and ⊕ signs are standard teaching in schools, colleges and universities around the world. Are you trolling? – tim Sep 07 '20 at 12:57
No, but people which think they know what is taught in other parts of the world do – schnedan Sep 07 '20 at 13:05
Well, a quick Google for [boolean algebra university slides](https://www.google.com/search?q=boolean+algebra+university+slides) sorted that one out. – tim Sep 07 '20 at 13:15
@schnedan (-1) The question is clearly involving the ⊕ and ≡ operators, which you don't get from simply grouping on a Karnaugh map. Your beloved [wikipedia](https://en.wikipedia.org/wiki/Exclusive_or) shows the disjunctive form of ⊕ as "x̅y+xy̅", which also wrecks your tangent about the plus operator. – mbedded Sep 08 '20 at 15:36
Well I don't see ⊕ and ≡ in the OP's formula plus these signs are just not common here - as well as + is not too. And its not my beloved wikipedia, I could also just scan a book I own for ~25 years with more or less the same content. Wikipedia is just more handy here. – schnedan Sep 08 '20 at 16:43

Simplify the boolean function $$Z=A\bar B \bar{C_i} + \bar A B \bar{C_i} + \bar A\bar B {C_i} + A B {C_i}$$

3 Answers3

Linked