Miller integrator ramp generator?

Question

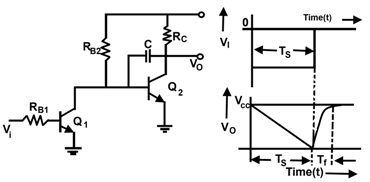
In a page on Ramp Generators I found this peculiar circuit which is said to be superb in its linearity. But I can't make sense of it. It doesn't discuss any of the actual R and C values.

I can see that Q1 and Q2 are mutually exclusive in on and off state. If V_i or what that means is above ground it turns Q1 on which turns Q2 off. The graph of V_i appears to say it should be negative, below 0V, but I already don't get why that should have to be the case? 0 is 0, off is off. Why negative on the base of an NPN?

Now I can see how C discharges through Q2. But Such discharge would be rapid. So how can that make a gradual and linear falling ramp as in the diagram? I suppose to do that the R_B2 must be only slightly on so current through the base of Q2 must be much limited.

I have experimented with that a little in LTspice, but it was hit and miss. And the charging time was considerable. I couldn't make Rc small enough before the linearity would disappear. How do you tune this thing?

And then I found another article which was a bit more complicated and used 4 different voltages. And there too I could not find any suggestions on how to choose the resistor values and the formula showed values that weren't even in the schematics (i.e., 2 capacitors when there was only one).

How do you dimension these things? I understand they may be only about principles, but I was intrigued by the simplicity of the first circuit and I could almost get it to work, but not fast enough for the 60 Hz that I need it.

Answer 1

In the first circuit you can assume the voltage at the base is (roughly) fixed and ignore base current, so use KCL to sum the currents at the base, and we get (Vcc - Vbe)/Rb2 = C * d/dt (Vc).

In reality the current gain is finite, and Vbe changes with collector current etc. so that equation is only an approximation. Higher values of Rc mean that the time to reset is longer but less base current is devoted to pulling current through Rc.

^{simulate this circuit – Schematic created using CircuitLab}

This might be a circuit that you could use to split nanoseconds (for example to avoid having an excessively high clock frequency yet maintain high resolution in a time counter). You could use a transistor with GHz ft in place of Q1 (all designators refer to original schematic).

To get a ramp time ~8ms, about 1000x longer than my example, you could use RB2 = Rc = 80K and C1 = 100nF.

Answer 2

I can't think of any good reason to use any of those circuits.

They have a very narrow design margin and are not scalable very far and work only at low frequencies. They integrate but do not dump properly as the switch does not go across the capacitor. Instead, it shuts off the 2nd stage and relies on the passive Rc pullup which also serves as only part of the ramp control.

The traditional way is to use a FET to dump the cap on a true OpAMp Integrator with a discharge time of Tau=Ron* Cfb

Although this is anecdotal, when I started out in design during the 70's I wanted to design a rocket Doppler tracking that gave a linear phase by using the edge of a received 100kHz from an OCXO PLL then used an edge of that zero-crossing signal to sample the phase of a local same frequency 100kHz sawtooth using a sample & hold. So I used a CMOS switch to multiplex between 2 sawtooths 180 deg. apart. so that no Ic=CdV/dt discharge was necessary. It just integrated a squarewave and used the inverted version each half cycle. The rocket motion in range would result in many cycles of Doppler position and the S&H difference frequency signal looked exactly as sharp as the original sawtooth, starting off from a flat line and accelerating up to Mach 7, 500 miles up then re-entering after scanning for aurora plasma dynamic properties. The slope of the resulting triangle change slopes as it counted down back to earth and the distance away for recovery was cycles converted to distance. Two antennae with a time-interval counter gave azimuth after signal processing.