0

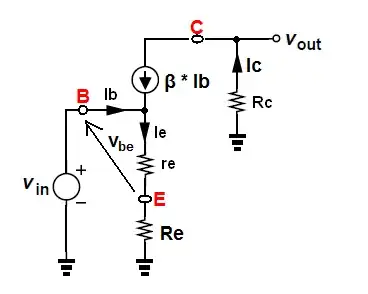
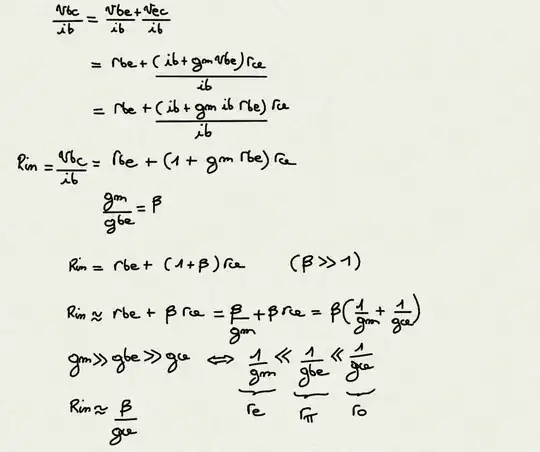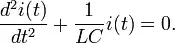I don't know to retrieve the \$r_\pi\$ value of common collector .

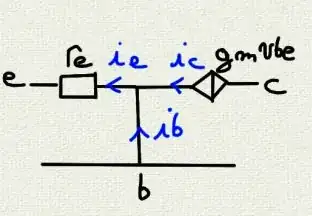
re model (or pi model) for common emitter configuration

Ok for \$r_\pi\$ model from common emitter with

enter image description here, enter image description here and enter image description here

re model for common collector configuration ?????

But to calculate $$ {v_{bc} \over i_b} = {\beta * r_e} $$ i don't know...

I get enter image description here and enter image description here

$$ {v_{bc} \over i_b} = {{v_{be}-v_{ce}} \over i_b} $$

Ok for \$ v_{be} = i_e \cdot r_e \$, but for \$ v_{ce} \$ ? Which is the voltage between the current source ?

re model for common base configuration

enter image description here, enter image description here, enter image description here

\$ R_{in} \$ for common collector configuration with hybrid h-parameters

It is easy with this technic but i don't find \$r_{be}\$

enter image description here,enter image description here

FALSE : $$ r_e \neq {1 \over g_m} $$

Putting a short circuit from e to c to get \$ R_{in} = \beta * r_e \$ for \$r_e\$ model for common collector configuration

putting \$r_o = 0\$ i get

enter image description here

but \$r_o\$ is big no ?

Putting \$ R_{L} \$ after the common collector configuration circuit to find \$r_e\$ model

enter image description here

cannot continue because 0 found

But with h-parameters : OK enter image description here enter image description here

Putting \$ R_{L} \$ after the common collector configuration circuit to find \$r_e\$ model with \$gm \ne {1 \over r_e}\$

enter image description here

enter image description here

Without \$ R_{L} \$ : \$r_{in}\$ of common collector configuration circuit with \$r_e\$ model (\$gm \ne {1 \over r_e}\$)

I don't understand why I have to add the mass to node e when I remove \$r_o\$, because finally it's like this I put the value of \$r_o\$ to 0.

Note : for the other circuits : Common Base, Common Emitter, i didn't need to do this trick adding a wire to make a circuit.

Why adding mass to calculate \$R_{in}\$ ?...

enter image description here

enter image description here

user7058377
  • 99
  • 6
  • 1
    Hmm, R_pi is always equal to: \$r_\pi = (\beta +1)r_e\$. So what is your problem? – G36 Aug 23 '20 at 20:11
  • You should care about \$v_{be}\$ value only, because the collector current is \$i_c = g_m v_{be}\$ – G36 Aug 23 '20 at 20:14
  • https://electronics.stackexchange.com/questions/476659/kvl-equations-for-this-small-signal-model/476666#476666 – G36 Aug 23 '20 at 20:20
  • 1
    Sounds like you are over thinking it. rE is 26 mV per mA of emitter/collector current at ambient temperature circa 27 degC. Anything more accurate is pointless for 99% of applications. – Andy aka Aug 23 '20 at 20:59
  • In fact the title : "re model of common collector" will be more appropriate. $$r_\pi = {v_{be} \over i_b}$$. I understand know that \$ r_\pi \$ is only used in this case – user7058377 Aug 23 '20 at 21:37
  • For common base configuration that you can see in demostration in the question : it is easy (like the C.E.). – user7058377 Aug 23 '20 at 21:50
  • @user7058377 why do you want to find Vbc voltage? If only Vbe voltage determines the collector current. – G36 Aug 24 '20 at 12:52
  • I want to find \$v_{bc} \over i_b\$ like the the demostration of Rin for common collector with the hybride h-parameters that i add in the question. – user7058377 Aug 24 '20 at 15:15
  • Simple short the output terminal (emitter to GND) in your "re" model and you will see that that \$R_{IN} =(\beta +1)r_e \$ because now you have an open circuit – G36 Aug 24 '20 at 16:01
  • If i am doing a short circuit instead of \$ r_o\$ it is like i am doing \$ r_o = 0 \$ : like the diagram introduced in the question – user7058377 Aug 24 '20 at 18:56
  • Now try to add a load resistance and try to find Rin. – G36 Aug 24 '20 at 19:35
  • I have tried but without success with \$r_e\$ model...OK with h-parameters (demostration in the question). – user7058377 Aug 25 '20 at 11:51
  • You wrongly assumed that \$g_m = \frac{1}{r_e}\$ which is not true. And that's why you got the wrong result. Remember that \$r_e = \frac{dV_{BE}}{dI_C} = \frac{V_T}{I_E}\$ but BJT's transconductance is equal to \$g_m = \frac{dI_C}{dV_{BE}} = \frac{I_C}{V_T}\$ from this \$g_m = \frac{\alpha}{re} = \frac{\beta}{r_{\pi}} = \frac{r_{\pi} - r_e}{r_{\pi} r_e} = \frac{\beta}{(\beta +1)r_e}\$ – G36 Aug 25 '20 at 13:38
  • I made a mistake in "re" definition. "re" is of course equal to \$r_e = \frac{dV_{BE}}{dI_E} = \frac{V_T}{I_E}\$ and because \$g_m\$ is \$g_m = \frac{I_C}{V_T}\$ addtional \$I_C = \alpha I_E \$ we have \$g_m =\frac{I_C}{V_T} = \frac{\alpha I_E}{V_T} = \frac{\alpha}{r_e} \$ – G36 Aug 25 '20 at 19:03
  • Thank You for your demonstration. I have done 2 trys (in the question) but I don't understand why I have to add the mass to node e when I remove \$r_o\$, because finally it's like this I put the value of \$r_o\$ to 0. Note : for the other circuits : Common Base, Common Emitter, i didn't need to do this trick adding a wire to make a circuit. – user7058377 Aug 27 '20 at 12:33
  • The answer is simple. If RE = 00 you have an open circuit. And in English w say ground (GND), not a "mass". – G36 Aug 27 '20 at 13:30
  • @Andyaka re 26 mV per mA -> shouldn't that be summat like 26 mV per ma'th. Or mVth per mA -> ie inverse relationship. Re falls as mA's rise. Re = 26/mA Ohms. || I know you know what you are intending to convey, but are you conveying it? – Russell McMahon Sep 12 '20 at 11:57
  • @RussellMcMahon yes it looks a little confusing.. \$r_E\$ is 26 mV divided by the emitter/collector current in mA hence if 2 mA flows, \$r_E\$ is 13 ohms. – Andy aka Sep 12 '20 at 12:00
  • @Andyaka I knew what you were intending to convey, but think the OP may not easily follow. || Fun factoid from this is the gain of a common emitter stage with no Re_external or with it bypassed is 38.4 x DC drop across collector resistor. So max possible gain of a common emitter stage (with no negative headroom at the limit is 38.4 x Vcc :-) . So eg a 9V supply CE stage has a realistic small signal max gain of ~~= around 300. – Russell McMahon Sep 12 '20 at 12:03

2 Answers2

2

To be honest I do not understand your problem. It seems that you are overthinking the problem. Stick to one single model and use it for all configurations (CC, CE, CB).

For example, you can use T-model. Thus for CC (emitter follower) amplifier, it will look like this:

enter image description here

In this model \$r_e\$ is equal to:

$$r_e = \frac{V_T}{I_E} = \frac{\alpha}{g_m} = \frac{r_{\pi}}{\beta +1}$$

And we alredy see that the voltage gain of a voltage follower is:

$$\frac{V_{OUT}}{V_{IN}} = \frac{R_E}{r_e + R_E}$$

We can use this model also for CE amplifier

enter image description here

For this circuit we have

$$V_{OUT} = -I_CR_C$$

$$V_{IN} = I_E\:r_e + I_E\:R_E$$

Aditional we know thet \$I_C = I_B*β\$ and \$I_e = I_B + I_C = I_B + I_B\:β = I_B(β + 1)\$

therefore \$ \large \frac{I_C}{I_E} = \frac{I_B\:β}{I_B(β + 1)} = \frac{β}{β + 1}\$

From this, we can write that \$I_C = I_E\frac{β}{β + 1}\$ thus we have:

$$V_{OUT} = -I_CR_C = -I_E\:R_C \:\frac{β}{β + 1}$$

And the voltage gain is:

$$\frac{V_{OUT}}{V_{IN}} = \frac{-I_E\:R_C \:\frac{β}{β + 1}}{I_E\:r_e + I_E\:R_E} = -\frac{R_C}{r_e +R_E} \:\frac{β}{β + 1}$$

As you can see we can use the same small-signal model for all amplifier configurations.

Of course, we can use a voltage-controlled current source model as well.

enter image description here

For example, the input resistance of this circuit is:

$$R_{IN} = \frac{r_e + R_E}{1 - g_m\:r_e} = (\beta +1)(r_e + R_E)$$

As homework try to prove that this formula is true.

Also, we can use a hybrid-pi model as well, see this example of CC amplifier

KVL equations for this small signal model

G36
  • 13,642
  • 1
  • 18
  • 33
0

What i understood (thanks to g36,...) are :

$$ {1 \over g_m} \ne r_e $$

See the very good paper here (thanks Prof.) to retrieve good technic to pass between \$r_{\pi}\$ and \$r_{e}\$ enter image description here

When searching parametters (like h-parametters) it is important to work with source and charge resistance and make a circuit (network which is closed)...

enter image description here

In final there are many similarities between h and re parametters.

user7058377
  • 99
  • 6
  • The H-parameters model comes from a two-port network theory where they treat BJT's like a black box. And this model has nothing to do with semiconductor physics. On the other hand for example the hybrid pi or T-model is highly related to semiconductor physics. Hybrid-pi/T-model is called a "physical model" because they more or less accurately reflect the "physics phenomenons" that occur inside the BJT. – G36 Sep 12 '20 at 15:08
  • H-parameter is supposed to be used for small-signal analysis and designing an amplifier circuit. But only in theory, in real-world we don't use H-parameters to design an amplifier. Only EE students are forced by their mad professors to use it. [H-parameters](http://www.talkingelectronics.com/Download%20eBooks/Principles%20of%20electronics/CH-24.pdf) – G36 Sep 12 '20 at 15:09