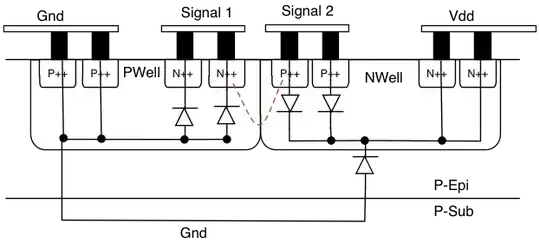
 The second figure is a modified version of the first figure.
The second figure is a modified version of the first figure.
In the second figure, how is the folded cascode stage formed by pnp transistors Q3 and Q4 used to raise the output resistance looking into the collector of Q4 to β4*ro4?
I have trouble understanding how β4*ro4 was derived.
The overall output resistance of the amplifier is: Ro = [β4ro4 || β5ro5/2]
I am referencing "Microelectronic Circuits" by Sedra and Smith, 7th edition page 654.