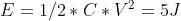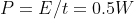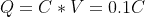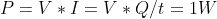Let's say I'm gonna charge a 1mF capacitor from 0 to 100V in 10 seconds. Assuming there's no limiting resistor nor any other losses, the total energy that must be tranfered from the 100VDC supply to the cap is:
So, the power transferred in 10 seconds:
Ok. The charge needed to charge the 1mF capacitor from 0 to 100V is:
So, the power transferred in 10 seconds is:
Which one is the correct? What did I do wrong?
Let's say I'm gonna charge a 1mF (1000 μF) capacitor from 0 to 100V in 10 seconds
That can be achieved with a constant current circuit in series with the capacitor fed from the 100 volt supply. The formula that defines the current is this: -
$$I = C\dfrac{ΔV}{Δt}$$
So, ΔV is 100 volts and Δt is 10 seconds. That means that I = 10 mA for a capacitance of 1000 μF.
From the perspective of the power supply, it is generating 100 volts and there is a load taking 10 mA, That's a constant power of 1 watt over the ten second period. If we converted power to energy (joules) by multiplying by time we get 10 joules.
But we also know the stored energy (W) of the capacitor when it reaches 100 volts: -
$$W = ½\cdot C\cdot V^2$$
Plugging the numbers in we get 5 joules. This means that 5 joules is converted to heat inside the constant current circuit.
Assuming there's no limiting resistor nor any other losses
That means you have made a contradiction in your question because you can't have a capacitor charging over ten seconds without some form of current limiting (be it a constant current source or a plain ordinary resistor). That current limiting consumes power. Neither can you instantly apply 100 volts to your capacitor because that implies infinite current and nobody has infinite current.
You can't eat your cake and have your cake.
You can of course play around with different times to construct a different scenario where the current is 100 mA or 1 amp or 10 amp etc. but, you'll always get the same result. Power transfer from a voltage source to a capacitor is not 100 % efficient.
Assuming there's no limiting resistor nor any other losses (again)
You can use an inductor in series with the capacitor. The inductor will soak up the energy that would have been turned to heat by the current limiter and thus prevent infinite current flowing. You will also need a diode so that once the capacitor has reached the "end-voltage" (and the inductor has transferred all the "soaked-up" energy into the capacitor), the capacitor remains charged.
This is how a boost switching regulator works and theoretically, it can operate at 100% energy transfer efficiency i.e. nothing wasted: -
Charging voltage reached is 200 volts from a 100 volt supply: -
So, with a 100 volts supply, the capacitor has charged to 200 volts and has done so with perfect efficiency. If you did the math you'd find that the final energy of the capacitor is 20 joules and that it took precisely 20 joules from the 100 volt supply.
