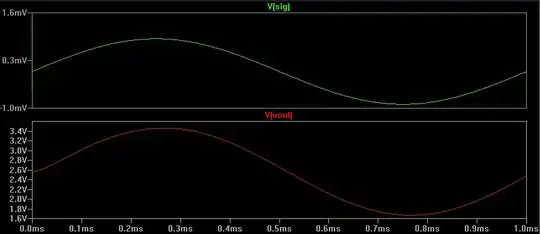
If the fundamental frequency of the two waveforms you are comparing is known, then a DFT of each, over samples for exactly one period will give you a nice complex number for each fundamental, whose argument (angle) can be calculated and subtracted for a phase difference.
You don't actually need a full FFT or DFT over the entire spectrum, you just require information for the fundamental, which can be obtained from just four simple O(n) operations. We do what the DFT algorithm does, but only for the fundamental component. For each signal, sample set \$v\$ (consisting of N samples), calculate:
$$ \sum^{N-1}_{n=0} v_ncos(\frac{2\pi n}{N}) $$
for the real part, and
$$ \sum^{N-1}_{n=0} v_nsin(\frac{2\pi n}{N}) $$
for the imaginary part. Then do the same for the second signal. Now you have two complex numbers, and you need to find the difference of their arguments, which will be phase difference in radians.
Notice that I didn't scale those values in any way, because you are not interested in amplitude, only phase.
Update: Doing this in real time isn't that difficult. This is just a sum of products. If you keep track of those products in a FIFO list of fixed length, then as each sample comes in you can update the total by subtracting the oldest product in the list, which is then "popped" and discarded, and adding the new product, which is then "pushed" into the list. Wow, that's difficult to explain in words.
If that sounds too complex (heh), and the signal isn't too noisy or harmnonically "busy" (if they are sinusoids, then it's easy), you could approach the problem with software-implemented hysteresis.
In software, mimic comparators with positive feedback (for hyseresis), in which you determine the instants in time when the comparators' outputs rise. The time difference between the rising edges is then the phase delay between the two signals.
For example, iterate the samples of a few periods of each, to find their maximum \$V_{MAX}\$ and minimum \$V_{MIN}\$ values. You then calculate hysteresis thresholds to be \$\frac{1}{3}\$ of the way between them, and \$\frac{2}{3}\$ of the way:
$$
\begin{aligned}
V_{L} &= V_{MIN} + \frac{1}{3} \left( V_{MAX} - V_{MIN} \right) \\ \\
V_{H} &= V_{MIN} + \frac{2}{3} \left( V_{MAX} - V_{MIN} \right) \\ \\
\end{aligned}
$$
Now iterate the samples again, setting a flag whenever a sample exceeds \$V_H\$, and clearing it when the sample value drops below \$V_L\$. Do that for the two signals you wish to compare. The number of samples between rising edges (the flags going high) for each is proportional to the delay between the two.
To perform this in real-time, keep track of peaks and troughs in the waveforms as the samples come in, updating \$V_{MAX}\$ and \$V_{MIN}\$, and recalculating \$V_L\$ and \$V_H\$ accordingly. You could implement some kind of moving average to follow \$V_{MAX}\$ and \$V_{MIN}\$ over time.
This may not be as accurate as a DFT, because it's more sensitive to noise, but it's pretty simple, and works without any knowledge of the frequencies involved. In fact, you can determine frequency also from those edges.