Settling time in 2nd order response (circuit)

Question

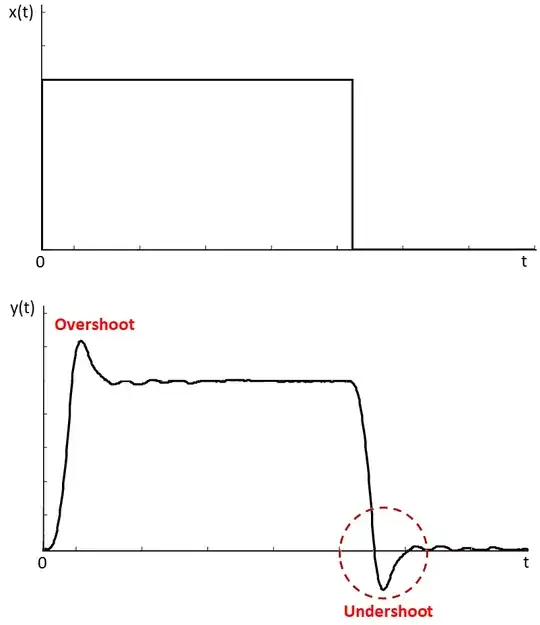
I understand the definition of settling time defined as "time took to reach within +-2% (or 5) of the converged value". Then does it mean settling time cannot be defined when the response converges to zero?

Answer 1

For the sake of simplicity, consider the standard second order transfer function (can be expanded to higher orders, too), including a DC gain:

$$ \frac{Y(s)}{X(s)}=\frac{G_{DC}\omega_n^2 }{s^2+2\zeta\omega_ns+\omega_n^2 } $$

A typical response to a rectangular pulse applied on input is shown below. highlighting a possible occurrence of overshoot and undershoot:

In time domain, the differential equation representation is:

$$ \frac{1}{\omega_n^2}\frac{d^2}{dt^2}y(t)+\frac{2\zeta}{\omega_n}\frac{d}{dt}y(t)+y(t)= G_{DC}x(t) $$

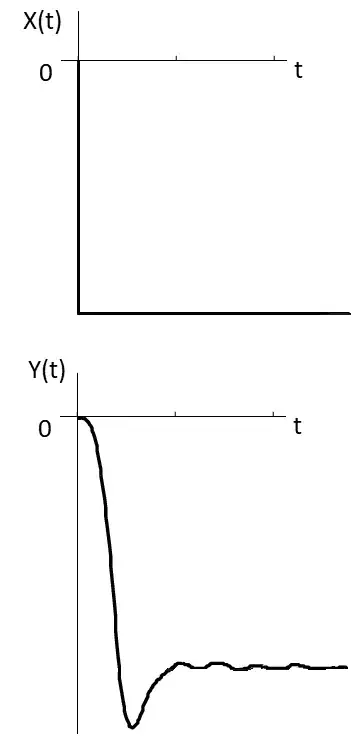
For the undershoot, we can imagine a new time line, starting when the input pulse goes to zero. Although we often examine the step input, which is customarily taken in a positive direction, we can also use the step signals in a negative direction. I'll show as that undershoot despicted on figure can be translated as a negative input step with a the correponding effect on system output. After the initial overshoot, the system is in steady state and all derivatives on differential equation are zero, leading to (remember the new time line):

$$ y_0 = G_{DC}x_0 $$

Subtracting this expression. from the differential equation (note that derivatives of constants are zero):

$$ \frac{1}{\omega_n^2}\frac{d^2}{dt^2}\left(y(t)-y_0\right)+\frac{2\zeta}{\omega_n}\frac{d}{dt}\left(y(t)-y_0\right)+(y(t)-y_0)= G_{DC}(x(t)-x_0) $$

Now, change the variables to:

$$ \left\{ \begin{array}{cl} X(t) = x(t) - x_0 \\ Y(t) = y(t) - y_0 \end{array} \right. $$

Resulting in a new and equivalent diff. equation:

$$ \frac{1}{\omega_n^2}\frac{d^2}{dt^2}Y(t)+\frac{2\zeta}{\omega_n}\frac{d}{dt}Y(t)+Y(t)= G_{DC}X(t) $$

On undershoot, for this particular case, the \$x_0\$ and \$y_0\$ are positive values and the steady state ones (final \$x(t)\$ and \$y(t)\$ are zero). The response in terms of \$X(t)\$ and \$Y(t)\$ (non zero steady state values) is shown below:

A linear system obeys the homogeneity principle - when the input t is multplied by a constant, then the corresponding output also is (in this case, a negative one). So, with the proper scaling, you could estimate the settling time based on undershoot, too (for example, if you only knew this part of the graph). Conclusion: As stated by others in comments: For a linear system, in order to investigate the effect of steps, it's importante to know the VARIATIONS on input and output.