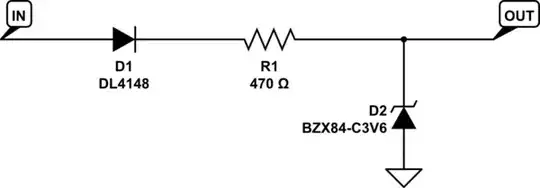
how does my signal source see the whole cable?
Let's start with simple, lossless, uniform, coax. There are more complicated systems that other people will be able to tell you about.
If the cable is terminated in its characteristic impedance, which we'll assume is 50 Ω, then the cable input looks like 50 Ω. The important thing here is that for lossless cable, that's true for any waveform, at all frequencies including DC, and for any length of cable.
simulate this circuit – Schematic created using CircuitLab
Here are two ways we might describe a transmission line line as 'terminated' (there are others). In your comments, you talk about using 3m of RG316 coax cable. This length has a loop resistance of about 1 Ω, while the cable has an impedance tolerance of about 2 Ω.
In the upper diagram, the opamp will see a load of about 25 Ω. This will be essentially resistive from DC to 100 MHz. Any capacitive or inductive component will be insignificant. Very few common amplifiers will be able to drive this without trouble.
In the lower diagram, the opamp will see a load of about 100 Ω from DC to 100 MHz, with the same caveats.
We use slightly different models to explain time domain and frequency domain behaviour. Time domain involves steps and impulses in time, which have a very wide frequency spectrum. Frequency domain descriptions tend to use single frequencies, which focus on long term behaviour and ignore the initial transient. Remember they are both true, and any apparent conflict is one of language and the model's domain.
If we throw a step input at the cable, so a broad range of frequencies including very high frequencies, the cable input looks like 50 Ω initially. It looks like 50 Ω for as long as it takes the step wave to reach the far end of the cable. If it finds 50 Ω there, it doesn't get reflected, and the cable input continues to look like 50 Ω indefinitely.
If the step finds an open circuit, then it gets reflected voltage in phase, current in antiphase, and when the step reaches the input again, the voltage doubles and the input current drops to zero. At low frequencies in the frequency domain, when the cable transit time is very short compared to the period of the signal, this open circuit behaviour looks capacitive at the input. With a short circuit on the output, the low frequency input behaviour looks inductive.
With a long line, the behaviour is more interesting. If the output is open circuit, then at a frequency for which the line is a quarter wavelength long, the input actually looks like a short circuit. This special line length is much used in filters and other components as this impedance transformation is so useful. However, whatever the frequency in the frequency domain, an open circuited 50 Ω line will never look like 50 Ω at the input, only short, open, inductive or capacitive depending on the length and frequency.
With a lossy line, the behaviour is more complicated. Once the series resistance becomes a significant fraction of the impedance, it can no longer be ignored. This is complicated by the fact that at RF, the skin depth effect increases the effective resistance.