1

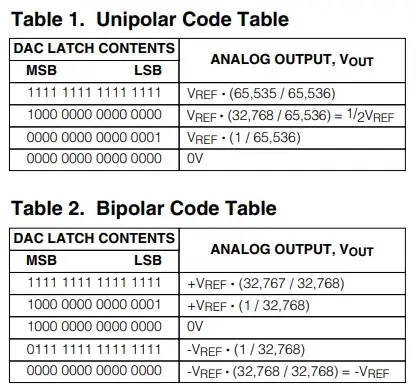
I am looking for the formula for an ideal DAC: a device that takes in a digital code and returns an analog value

rfwireless-world.com claims

$$V_{out} = D\cdot V_{ref}/(2^N-1)$$

where D is the digital code and N is the resolution of the DAC.

However, sciencedirect.com claims it is

$$V_{out} = D \cdot V_{ref}/2^N$$

Which is correct? The second equation seems to imply that \$V_{out}\$ will never equal \$V_{ref}\$ since the highest value \$D\$ can take is \$D_{max} = 2^N-1\$

john morrison
  • 25
  • 3
  • 2
    There is an answered duplicate question somewhere on this site. – DKNguyen Jun 02 '20 at 23:00
  • 2
    There's a similar area of confusion for ADCs: https://electronics.stackexchange.com/questions/462522/adc-first-transition-at-1-2-lsb-is-that-not-a-non-linearity/462528#462528 – MarkU Jun 02 '20 at 23:39
  • @john morrisson , please see my answer in:https://electronics.stackexchange.com/a/387507/22676 – Dirceu Rodrigues Jr Jun 03 '20 at 02:26

2 Answers2

4

This is the classic 'fencepost problem'. \$2^N\$ is the number of codes, and \$2^N-1\$ is the number of steps between codes. Since the MSB transition is defined as \$V_{ref}/{2}\$, the full-scale code falls just one step short of \$V_{ref}\$.

edit:

Here's an example, taken from the MAX541 datasheet (full disclosure: I am an applications engineer at Maxim Integrated): https://datasheets.maximintegrated.com/en/ds/MAX541-MAX542.pdf

MAX541 Table 1 Unipolar Code Table, Table 2 Bipolar Code Table

Note the full-scale value for analog output is 65535/65536 of VREF, or 32767/32768 of VREF, depending on configuration.

MarkU
  • 14,413
  • 1
  • 34
  • 53
  • That would mean that the second equation is the correct one, right? In other words, a code of all ones "1111...." would be smaller than Vref by \$V_{ref}/2^N = V_{LSB}\$? – john morrison Jun 02 '20 at 23:24
  • 1
    And I think I just thought of an obvious way to answer the problem. Since code 0 corresponds to an output of 0, we have \$2^N-1\$ codes remaining. Since each code spans 1 LSB, the final code must correspond to \$(2^N-1)V_{LSB}\$. This immediately rules out the first equation. Perhaps this is equivalent to what you were saying? – john morrison Jun 02 '20 at 23:34
0
   n bits = 2
   4      Nref
   3   11 Nmax
   2   10 
   1   01 
   0   00

$$N_{step} = 1$$ $$N_{step} = \frac {N_{ref}}{2^{n}} = \frac {N_{max}}{2^{n-1}}$$

RussellH
  • 12,496
  • 2
  • 9
  • 34