Why are two PID controllers needed for FOC (Field Oriented Control)?

Question

I've been looking at code to do FOC and noticed that two PID controllers are usually used for torque control -- one that keeps Id near zero and another that maximises Iq.

I understand why Id should be minimised and Iq should be maximised.

What I don't understand is why two PID controllers are needed to solve for what as I understand is essentially one unknown. My understanding (which probably needs correcting) is that the only goal of FOC is to figure out the torque and speed induced phase offset between the voltage and current which is caused by the windings' inductance and back-EMF.

If this is correct (that knowing this phase offset at any point in time would be enough to optimally determine what voltage to put on what windings) then why isn't there one PID loop which optimises for the percent of the output power that goes to Iq? Something like trying to get Iq/(Id+Iq) to be as close to 1 as possible.

Answer 1

Step back and think what Id does for you and equally the relationship between Vd and Vq

Injection into the quadrature axis will facilitate torque production while injection into the direct access with facilitate field weakening.

To maximise the torque production you ideally want zero Id as a direct current component will result in a reduction in torque production. How? via a vector rotation. Id and Iq are always in quadrature and thus if there is some Id for a given Iq, the overall frame of reference must rotate.

The two PI(D) controllers within the FOC current loop take in a current error and produce a voltage demand. This Vd and Vq, via an inverse Clarke & Park produce the three phase voltage demands that shall be applied to the stator to facilitate current flow. As you increase in rotor velocity the displacement power factor increases as the \$j\omega_e L \$ vector length increase with regards to the \$V_{bemf} \$ and the IR vector. This natural rotation as to where the current shall be injected occurs as the Id component is kept as close to zero as possible (resulting in an increasing Vd term).

Lets look at this rotation.

The inverse Clarke & Park equations are such.

\$ V_a = V_d \cdot Cos\Theta - V_q\cdot Sin\Theta \$

\$ V_b = V_d \cdot Cos(\Theta - \frac{2\pi}{3}) - V_q\cdot Sin(\Theta - \frac{2\pi}{3}) \$

\$ V_c = V_d \cdot Cos(\Theta + \frac{2\pi}{3}) - V_q\cdot Sin(\Theta + \frac{2\pi}{3}) \$

for a "perfectly aligned" rotor and zero Vd component, the anticipated waveforms can be seen below

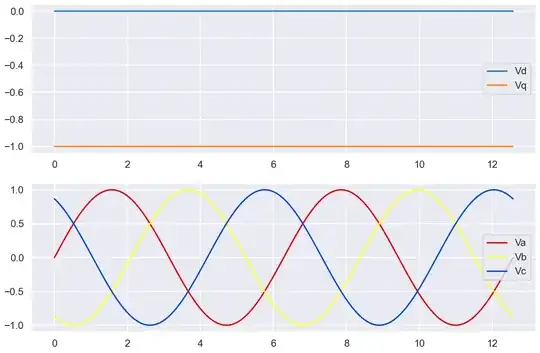
With a 20% Vd component added the waveforms can be seen below:

there is a clear phase-shift. If I overlay the two sets of Vabc it becomes very clear.

The waveforms now lead where they should be due to how a direct component rotates the vector. There is also a slight magnitude increase since the envelope of the 3phase sinewave follows \$\sqrt{V_d^2 + V_q^2}\$ and under current control the Vq component would have been reduced.

So it has been established that:

1. The output of the two current controllers is a voltage demand, a demand needed to cause the desired current to flow
2. A direct component causes a rotation (or a phase shift in the rotating 3phase domain)

then why isn't there one PID loop which optimises for the percent of the output power that goes to Iq? Something like trying to get Iq/(Id+Iq) to be as close to 1 as possible.

What would happen if aspects of Iq was used as the Id demand. For starters it would need to be aspects of Vq to influence Vd since the output of the PI(D) is voltage not current. What would happen if we had one PI controller that takes in an Iq demand and generates a Vq based upon the present Iq. From this produce Vd based upon say ... \$Vd = \frac{Vq}{Vd+Vq}\$ akin to the original query.

We would have a response which varies the phase relationship of the applied voltage based upon the quadrature current demand. Whenever there was a demand change or a load change the controllers response would result in a phase shift from the desired angle and thus compromise the ability of the system to generate torque effectively.

By implementing independent controllers for Id and Iq, their specific contributors to the overall system response can be controlled. Iq is free to change based upon a demand from an outer velocity loop while Id is controlled to rotate the vector due to any possible rotation due to acceleration or velocity.

Since Id (and thus Vd) has an impact of the torque angle, an Id demand can be used to produce field weakening to enable the system to reach higher velocities at the expense of torque production.

Answer 2

Disclaimer; I am no expert in FOC, But I have studiet it a bit, and this is my take on it;

(I have also used it, and studied the circuit implementations used)

What I don't understand is why two PID controllers are needed to solve for what as I understand is essentially one unknown.

It is not one unknown, it is two..

My understanding (which probably needs correcting) is that the only goal of FOC is to figure out the torque and speed induced phase offset between the voltage and current which is caused by the windings' inductance and back-EMF.

Im not sure I understand this sentence, but it seems to me like you think the only thing FOC takes care of is the phase, are you disregarding the amplitude?.

If this is correct (that knowing this phase offset at any point in time would be enough to optimally determine what voltage to put on what windings)

Again, why are you disregarding the amplitude?

then why isn't there one PID loop which optimises for the percent of the output power that goes to Iq? Something like trying to get Iq/(Id+Iq) to be as close to 1 as possible.

Have a look at the equation you wrote, and see what solutions get it to be as close to 1 as possible;

$$\frac{I_q}{I_d+I_q}=1\Rightarrow I_q=I_q+I_d\Rightarrow I_d=0$$

What I am trying to say is that this says nothing about the value of \$I_q\$, it could be anything. Or in other words; only making \$I_d\$ go to zero doesn't give you a point solution, it gives you a line.

From what I have read and understood about FOC, this is how it (usually) is implemented;

• There is an inner feedback-loop which controls the current (at any one point in time) by controlling the duty-cycle of the pwm output to the output stage transistors (with feedback from measuring the voltage across a current-sense resistor).

• Then there is an outer feedback-loop which takes care of the phase (making \$I_d\$ near zero), for this it uses feedback from an encoder to get the angular velocity.

So it has two feedback-variables; 1) current through the windings, and 2) angular-velocity.

Each is used as feedback to its own feedback-loop, the outer loop is what is used to control either the resulting velocity or applied torque

Often there is then actually a third control loop around that, which allows you to control the target position.

Answer 3

To commute a BLDC motor, you don't need either PID loop. Take them out and feed a constant into your inverse park -> inverse clarke/SVM, your motor will spin. This is called 'sinusoidal' control, and with a nonzero constant \$I_q\$ and zero \$I_d\$ (\$V_q\$ and \$V_d\$ would be more semantically accurate) it'll be like a brushed DC motor. FOC doesn't need to measure phase voltage/back-emf at all. In its simplest form, you're just figuring out where the rotor magnets are relative to the stator (the all important electrical angle) and then setting 3 voltage levels that will optimally produce torque at that angle.

A motor is a machine that converts current into torque. The PID loops are there because in the condition of maximum efficiency of a PMSM, \$I_q\$ is a flat constant and \$I_d\$ is zero. Those two PID loops are there to attempt to maintain that condition and minimize disturbances caused by physical artifacts of the motor's construction.

Answer 4

Although I'm not an expert to answer this, I can try to explain it according to what I know. BLDC motors are three-phase induction motors basically. The three inputs require perfect sinusoidal to work properly, separated at a 120-degree phase. For FOC, providing maximum torque voltage needs to be applied to the coil perpendicular to the rotor magnetic field. Only, in that case, torque will be maximum. To apply a proper potential across the correct coil, it needs to know the orientation of the rotor magnetic field. To calculate the proper orientation PID must be used to control the voltage accordingly for a steady torque. Apart from field orientation, as the rotor is basically an inductor, there is a 90-degree phase shift of current with voltage. So the controller needs to also monitor current consumption using PID to properly apply a voltage across the coil for a stable and steady rotor speed and torque. Thus two PID controllers are required. I hope this thing will clear your doubt. If you've any doubt, I can try my best to help you.

Answer 5

The simple answer is that PID itself is not really related to FOC.

You can imagine a brushed DC motor, it's way simpler- just one phase, one current, still a PI or PID controller is used for the current control. The reason is that it's the simplest way to achieve torque required for certain motion.

The system normally builds a motion profile, dictated by simple physical properties of the mechanics- speed, acceleration, etc. Requirement of certain acceleration means on the electric side the proportional current. But is not related to anything else, while your output is voltage- just because this is how it works. So the optimal way is to "find out" what voltage should be applied to have this current, and a "finding out" mechanism is a PI or PID controller.

How does a DC brushed motor create a rotating magnetic field? It uses a mechanical commutator. In a brushless motor you don't have that, instead you represent the field by two vectors- Iq and Id. Basically Iq is the same controller you had in the DC brushed, Id is the way to set the angle.

If you would have a different way to control the current (i don't know, a neuron network maybe), you could use it as well. It's not about PID, it's about the control.

UPD: i have re-read the post, and it seems that maybe you ask why two controllers, rather than one- so it's because there is a rotating vector, that is two-dimensional. Easiest to imaging as a rotating arrow starting on the axis and pointing to some point relative to the rotor. The rotor has a sine field of itself, which is fixed to it. As the rotor goes, you measure it's position and feed it to the controller of Id and Iq, and the control the rotating field to match the rotor position.