What is commercially called a hub dynamo is more accurately described as a magneto, or even more accurately as a permanent magnet synchronous machine.
The terminal voltage of a magneto is related to the change in magnetic flux linked through the coil by
$$v = -N\frac{d\phi}{dt}$$
The flux linking the magneto coil is made up of two components. One component is the flux induced by the permanent magnet linking the coil. The other component is the flux induced by current flowing through the coil. All of the flux induced by current through the coil also links the coil. We will call the linked flux induced by the permanent magnet \$m(t)\$. The flux induced by the current \$i\$ is proportional to \$i\$, so call it \$ki\$. Then,
$$\phi = m(t) + ki$$
If the coil is open, and no current is flowing, the only flux component is from the permanent magnet. The faster the magnet (or magnets) rotate, the higher the rate of change of flux and the higher the open circuit voltage. This video shows the open circuit voltage generated by a hub dynamo increasing linearly to 100v (corresponding to a bicycle velocity of about 100km).
Automotive (and bicycle) synchronous machines are often regulated with shunt regulators. A Zener diode can be used as a simple shunt regulator, but it needs to have sufficient power rating. More complex shunt regulators often use power transistors. We will be especially interested to know how much extra power is dissipated by a shunt regulator when the speed of the magneto is increased.
If the voltage across the magneto's terminals is held to \$v_{max}\$ then the the rate of change of flux is given by
$$\phi' = -\frac{v_{max}}{N}$$
Integrating, we have
$$\phi = -\frac{1}{N}v_{max}t + C$$
So we have
$$-\frac{1}{N}v_{max}t + C = m(t) + ki$$
We can visualize this result by performing a simulation. We note that the shape of the flux wave induced by the permanent magnet(s) gets scaled on the time axis as the rotor speed increases, but is unchanged on the amplitude axis. This is similar to the effect of applying a constant rms amplitude alternating current to the primary of a transformer. Thus our simulation model can be something like this:
simulate this circuit – Schematic created using CircuitLab
The following diagrams show the open-circuit output voltage with the Zener diode D3 REMOVED, at an input frequency of 10Hz, 100Hz, and 1000Hz.
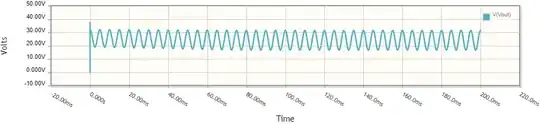
Those diagrams show the unregulated voltage increasing linearly with frequency, to a very high voltage of approximately 300V!
Next, here is what happens when a shunt regulator is present (in this case a 6V Zener diode). First at 100Hz.
Notice that the output voltage remains near 6V and the current oscillates with a peak of around 200 mA.
Now comes the perhaps surprising result at 1000Hz.
Once again, the voltage is about 6V and the peak current is about 200mA.
Thus, what we see is this.
- When there is no shunt regulator present, the terminal voltage will increase linearly with the rotor speed.
- The output voltage may be held constant by using a shunt regulator
- When the output voltage is held constant by using a shunt voltage regulator, and the rotor speed is sufficient, the magneto current becomes independent of rotor speed (or at least approximately so).
From what others here have said the regulator is a Zener diode.
It might be, if the Zener is rated sufficiently to handle the maximum rated current of the magneto (hub dynamo) at the rated voltage. Otherwise, the regulator may be a shunt regulator employing a power transistor.
by using the regulator is all the energy being generated when I ride at greater than 10 km/h being burnt in the regulator. Isn't this a very wasteful way of dealing with the higher voltage.
As seen above, although the unregulated voltage increases with speed, the magneto's terminal voltage may be regulated with a shunt regulator. When regulated with a shunt regulator, there is a maximum electrical power that will be generated, regardless of rotor speed. Some of that power may be dissipated by a light or other device. The excess power (i.e. the relatively fixed power generated minus the power used by devices) will be dissipated by the shunt regulator.