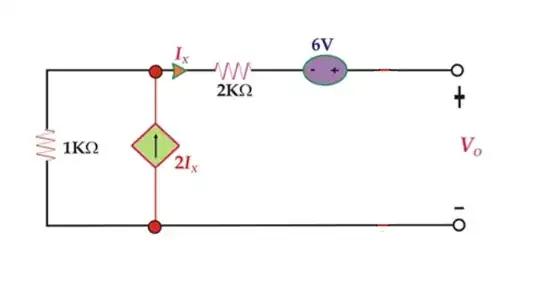
In AoE3 2.3.5.C (page98) it states the following (referring to the circuit in the image):
For instance, feedback acts to reduce the input and output impedances. The input signal sees \$R_1\$ resistance effectively reduced by the voltage gain of the stage. In this case it is equivalent to a resistor of about 200\$\Omega\$ to ground (not pleasant at all!)...
The intrinsic emitter resistance \$r_e\$ is \$\frac{V_T}{I_E} = 25.3\Omega\$ (with \$V_T \approx 25.3mV\$). Only \$R_2\$ and \$r_e\$ are "to ground" so \$R_1\$ does not play in the part. So \$R_{R2||(\beta*re)} = 1844\Omega\$ (with \$\beta \approx 100\$), and hence the signal input impedance. I can't understand how input impedance is reduced to 200\$\Omega\$ in this grounded emitter amplifier circuit with DC feedback.