4

The MOSFET's turn on/off curves have a part where the drain current and the voltage across Drain-Source are not zero. That's where most of the switching dissipation happens.

The problem I have is in T1-T2 section (see figure below). If the source voltage (Vin) is constant and the current is flowing through the load (ILOAD), how can we still have Vin across Vds?

We shouldn't have the same current flowing through the load when Vds=0 and Vds=Vin ...

Can you please explain what am I missing?

Does this logic differ with a different source type, a different load type ... What are the parameters I need to properly predict the MOSFET's behavior when turning on/off, other than the gate driving?

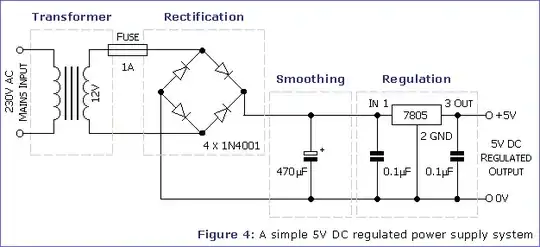
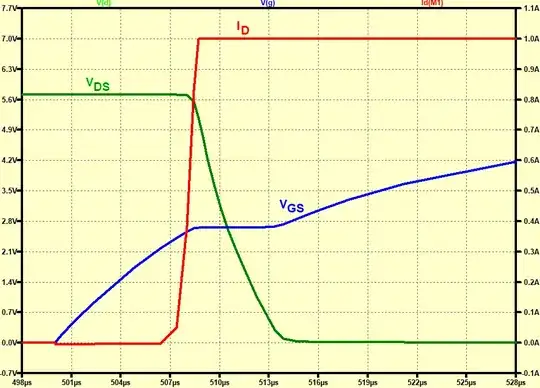
enter image description here

https://www.vishay.com/docs/68214/turnonprocess.pdf

Image taken from a Vishay application note

HatimB
  • 826
  • 5
  • 15
  • If there was a circuit diagram from that application note that they reference, it would help to also include this in question post. what is VIN exactly? – Leoman12 Apr 25 '20 at 22:32
  • Thank you @Leoman12 for the comment, I added the circuit as well as a link to the app note – HatimB Apr 25 '20 at 22:38
  • This might be wrong but I’ll give it a try. I think it’s important to notice that this is an inductive load. For a step voltage input to a inductive load, the response is that the inductor current rises exponentially or almost linear if quick enough. But voltage across inductor changes almost instantaneously. This isn’t right but maybe someone can explain it. A resistive load would have curves like in figure 10 from here https://assets.nexperia.com/documents/application-note/AN11158.pdf – Leoman12 Apr 25 '20 at 22:51
  • This is actually a good question. I can’t answer because I myself don’t know. But if no one answers this, I’d recommend contacting VISHAY and ask them about this. They’ll probably be happy to explain it because it’s their document. – Leoman12 Apr 26 '20 at 00:39

3 Answers3

5

The answer is that all these plot shows in application notes are made by assuming the inductive load plus a flyback diode is switching by a MOSFET. As shown in fig 6.

Additionally, the authors assume the MOSFET operates as a switch in the application when the inductive load is in "continuous current mode"(we replace the induction with a constant current source at the drain for this purpose). Thus, the current in the flyback diode and in the inductor is not at 0A at the beginning of a turn-on process.

And due to the flyback diode current, the MOSFET Vds will start to decrease only when diode current reach 0A (the MOSFET needs to take over all the inductor current from the diode) before Vds starts to decreases.

And the simulations confirm this:

enter image description here

Try read here

https://www.allaboutcircuits.com/technical-articles/switching-losses-effects-on-semiconductors/

But of course, for a pure resistance load, the situation looks different.

enter image description here

As you can see for a purely resistive load everything looks as we expect to be looking.

Bruce Abbott
  • 55,540
  • 1
  • 47
  • 89
G36
  • 13,642
  • 1
  • 18
  • 33
1

The curves for figure 7 do not match the schematic of figure 6, they are both generic diagrams and not intended to be read together.

Figure 7 is intended to show the gate charge, while turning on into a 'maximally difficult' load, that is one that draws, or may draw, a lot of current before the drain voltage drops.

In the case of the figure 6 inductive load, Iload will stay quite low through to T3, as it's not until a voltage is applied across a load inductor for some time that any significant load current starts to flow.

The sort of load that could generate the figure 7 curves would be a parallel RC, where the C takes a significant charging current to change its voltage at all.

T0-T1, Vgs is sub-threshhold, nothing happens. Vgs is increasing as the FET driver pushes current into the small Cgs capacitance.

T1-T2, Vgs causes the FET to start to turn on as a current source, Ids is more or less independent of Vds. T2 is defined by when Vds starts to drop. With an inductive load like fig 6, it will drop very early, as Ids will still be low. With a large capacitive load, T2 will be later at a higher Ids.

T2-T3, this is the Miller Plateau. Even though Cdg is often fairly small, the fact that it's connect to the drain, which has to make a large voltage excursion from rail to ground over this time, means that the gate drive current has to push a lot of charge into Cdg. The FET is behaving at this point as a linear amplifier, and the feedback through Cdg produces a 'virtual ground' at the gate terminal, which is why Vgs is barely changing in this region.

T1 through to T3 is a 'bad place' for the FET to be thermally, with high heating in the channel. This is what the SOA graph is for, to see how long the FET can be allowed to dwell in this high power region.

T3-T4, finally the FET is on. The channel is no longer dissipating high power. Vgs rises to the final gate drive voltage.

Neil_UK
  • 158,152
  • 3
  • 173
  • 387
0

no , it switch mode T0: VGS=0 ; Vds == Vin , T0-T1 - its a front of turn ON impulse, expanding\exagerated, so capacitors inside mosfet starting to change conditions. an T1-T2 begin of changing state, graph Vin - actually level of feeding\power voltage, it not changing, but Vds falling from Vin level, (a bit wrong diagram, Vin need a horizontal dash line) T2-T3 are really small, it significantly exaggerated there

JamesBrown
  • 76
  • 3