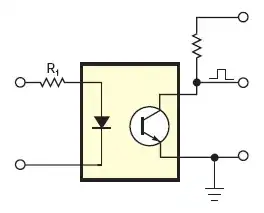
The Ebers-Moll equation is given by:$$I_C = I_S(T) * (e^{V_{BE}/V_T})$$ where \$V_T\$ = \$kT/q\$ = 25.3mV at room temperature. In TAOE (2.3.1), it mentioned
\$I_S(T)\$ is the saturation current of the particular transistor (which depends strongly on temperature, T ... \$I_S(T)\$ approximates the reverse leakage current (roughly \$10^{-15}\$A for a small signal transistor like the 2N3904.
I ran a simple simulation just to test the Ebers-Moll equation, where \$I_C\$ is just approximated to \$10^{-15}\$A, and taking \$V_{BE}\$'s value directly from the simulation: $$I_C = 10^{-15} * e^{0.727330 \div 0.0253} = 0.003A \ \ or \ \ 3mA$$
The value is over two orders to one simulated by the program iCircuit (427.267mA). If I just use KVL and multiply the default \$\beta\$ of 100, I get \$I_C = (5-0.727330) \ \div \ 1000 * \beta = 0.427262A \ \ or \ \ 427.267mA\$ matching that in the simulation. How am I supposed to use Ebers-Moll equation and why is it more accurate to determine collector current by base-to-emitter voltage. I just plug in some basic values in and the result did not even turn out close.