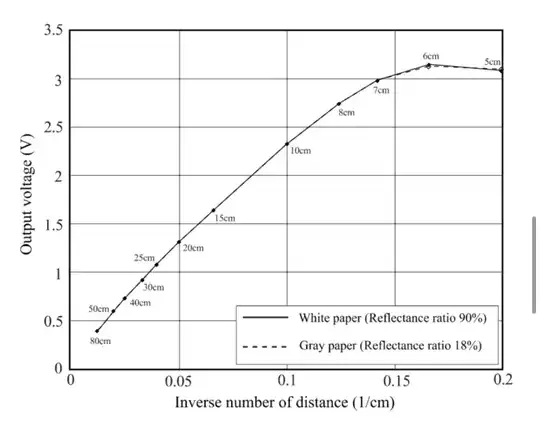
Please is this graph for voltage against distance linear or nonlinear
Asked
Active
Viewed 142 times
-2
Tukoor
- 7
- 3
-
that graph is voltage against inverse of distance ... draw the graph as voltage against distance and look at it – jsotola Apr 19 '20 at 03:06
-
Linear means straight line. Constant rate of change – relayman357 Apr 19 '20 at 03:14
-
Okay thank you. – Tukoor Apr 19 '20 at 03:49
-
I think, constant rate of change is not enough. The function y=ax+b has a constant slope - however, it does not fulfill the linearity condition (see wikipedia) – LvW Apr 20 '20 at 07:33
-
@LvW the \$y=ax+b\$ type of function is called affine, in many contexts it works pretty much the same as a linear function (just discount the offset). – jDAQ Apr 20 '20 at 07:56
-
jDAQ - yes, that is right. I works linear for delta values. – LvW Apr 20 '20 at 17:26
3 Answers
0
The graph is linear. When an increase in 1 of the x value results in an increase of a y value by a constant amount, that means it is linear. The graph deviates from this linearity a little after, but for the most part it is clear that the graph is straight, so it is therefore linear.
Jared Cohen
- 248
- 1
- 11
0
Its linear where ever its a straigt line between two points. Overall this graph is non linear because it doesnt look like a straight line from beginning to end.
Alex
- 1,018
- 2
- 12
- 26
0
The graph does NOT satisfy the linearity condition f(x+y)=f(x)+f(y).
Hence, the graph is non-linear. This applies even for output voltages below 1 Volt because a continuation of the graph with a straight line will not cross the origin.
LvW
- 24,857
- 2
- 23
- 52
-
If your are talking about mathematics, sure, but colloquially\practically people refer to linear as two things that have $$ \frac{f(x+t)-f(x)}{x+t-x} = c $$ that is the input and the output vary linearly, very good for sensors and approximations. – jDAQ Apr 20 '20 at 07:59
-
In such a case we speak of "piecewise" linear. However, the question is if this case applies to the shown function. I don`t think so. Even in case of a small non-linearity we cannot speak about a linear function - we also can say that it is "good enough" because in practice no physical characteristic is really linear in a mathematical sense. – LvW Apr 20 '20 at 08:52
-
I think you are being mathematically rigorous to an "experimental" plot, which sounds overthinking it to me, also "A piecewise linear function is a function defined on a (possibly unbounded) interval of real numbers, such that there is a collection of intervals on each of which the function is an affine function." so what I showed is not a piecewise definition, but a single linear/affine relation. All in all, I think you are being mathematically strict where you shouldn't, check this https://electronics.stackexchange.com/questions/128897/why-is-the-linearity-of-a-sensor-a-desirable-feature – jDAQ Apr 20 '20 at 15:08
-
Mmmmhh.. hard do judge if I am allowed or not...it sems to be a (nearly) philosophical question. You think, that I should not - why not? Do you know the background of the OP`s question - and how exact the expected answer should be? Nevertheless, I agree with you that my position is "mathematically rigorous". – LvW Apr 20 '20 at 17:30
-
Never said you're not allowed to, nor I think this is a philosophical matter. If the OP was looking for maths he would use MathSE, nothing in his question is about EE, its about reading plots. If you would like to use rigorous mathematics, why not mention that the slope completely changes after x=0.15? Well, because if you had a sensor like this, in engineering, you know that every sensor will have an offset, no matter how "linear" it is, and that the sensor is only "linear" in a certain range. In a engineering context "linear" usually means the variation is proportional, an affine function. – jDAQ Apr 20 '20 at 18:42
-
Simple answer: When I see the plot of a function that is non-linear - and when I am asked, if this is linear or not, what should be my first response? I am sure - when the OP has a certain engineering background he will be able to interprete the answer correctly. – LvW Apr 21 '20 at 07:56