How to find the cutoff frequency of an underdamped second order low pass filter?

Question

I've learned that for a first order low pass filter (LPF) the 3 dB frequency is one where the amp's gain is (surprise) -3 dB below the DC gain. However, on a second order LPF that is underdamped we get a "peak" at around the cutoff frequency which seems to throw that simple definition off...

For example, take the following filter:

Which has the frequency response of:

$$ H(j\omega) = \frac{1}{1 + j\omega \frac{L}{R} -\omega ^2LC} $$

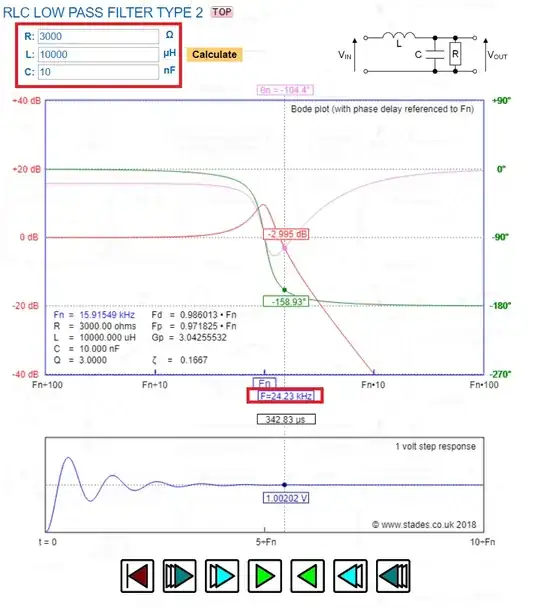
Running a Pspice simulation to calculate the cutoff frequency nets you the following result:

The gain at that frequency is a curious 6.6 dB. In contrast, for a resistor value of 500 ohms the system becomes critically damped and the cutoff frequency found by the simulation aligns with the simple definition I mentioned above.

How is the cutoff frequency defined in cases such as this? How does one go about justifying this simulation result, analytically calculating the above cutoff frequency?

Answer 1

The transfer function of this \$RLC\$ filter can be represented with a factored denominator featuring a quality factor \$Q\$ and a resonant frequency \$\omega_0\$: \$H(s)=\frac{1}{1+\frac{s}{\omega_0Q}+(\frac{s}{\omega_0})^2}\$. In this expression, \$\omega_0\$ represents the natural resonant frequency: it is the frequency at which the network rings for an infinite quality factor. It is also found under the term undamped resonant frequency. With this simple circuit built with perfect energy-storage elements (no losses in \$L\$ and \$C\$), it is classically defined as \$f_0=\frac{1}{2\pi L_2C_1}\$, \$L_2\$ being your inductor.

The peak you observe is due to the quality factor \$Q\$ defined by \$Q=R_1\sqrt{\frac{C_1}{L_2}}\$. Its value determines where the poles are located in the \$s\$-plane:

1. \$Q\$ is less than 0.5: you have to real roots and the response to an input step is non-oscillatory. When \$Q\$ is much smaller than 0.5 (0.01 for instance), then the filter response can be approximated by two cascaded poles, one dominating the low-frequency response while the second is in high frequency. This is the low-\$Q\$ approximation you can look up in the Internet.
2. \$Q=0.5\$, the roots are real and coincident: the response to a step input is fast and non ringing.
3. \$Q\$ is more than 0.5 then the roots are conjugated and the response is a damped oscillatory waveform. The frequency of the oscillation is no longer the natural ones but depend on the damping ratio hence the term damped resonance frequency defined as \$\omega_d=\omega_0\sqrt{1-\zeta^2}\$. As \$Q\$ increases, the poles approach the imaginary axis and the response to a step input is less and less damped.
4. \$Q\$ is infinite and the pole are located right in the imaginary axis and the response is a permanent oscillation tuned at \$\omega_0\$.

In your circuit, you can run a transient analysis and replace the ac stimulus by a PWL source delivering a 1-V pulse. If you observe the output voltage, then you'll either see a damped sluggish response for very low value of \$R_1\$, then set \$R_1\$ to 500 \$\Omega\$ and \$Q\$ is 0.5: the response is fast but still not ringing. Increase \$R_1\$ and you'll start seeing damped oscillations as \$Q\$ is getting higher.

The peak you measure in dB is directly the quality factor considering a 0-dB gain in this example. For instance, if \$R_1\$ is 2 k\$\Omega\$, the \$Q\$ is 2 or 6 dB.

Now the question was also about the -3dB-cutoff frequency. How do we obtain it from the transfer function? Simply derive the magnitude expression from the Laplace transfer function (replace \$s\$ by \$j\omega\$) by collecting real and imaginary parts. Then solve for the value of \$\omega_c\$ bringing the magnitude of the transfer function to 0.707: \$|H(\omega_c)|=\frac{1}{\sqrt{2}}\$. You can do it with the squared magnitude of the denominator equal to 2:

So for a load of 3 k\$\Omega\$ the -3-dB cutoff frequency is 24.2 kHz and it becomes 10.2 kHz for a 500-\$\Omega\$ load.

Addition:

Below the calculation sheet and the plotted transfer function where the 3-dB cutoff frequency is 24 kHz for a 3-k\$\Omega\$ load:

A quick SPICE simulation centered around the cutoff frequency confirms this number:

Answer 2

Using a tool

I get 24.23 kHz for the 3 dB frequency when R = 3000 ohms using this on-line tool: -

Other useful information: -

• The peak amplitude is 9.665 dB (at 15.46 kHz) and not the 6.6 dB mentioned in the question. See \$G_P\$ = 3.04256 = 9.665 dB.
• The peak occurs at 0.971825 of \$F_n\$ = 15.467 kHz
• If a calculation is made for the natural resonant frequency you'd use this formula: -

$$f_n = \dfrac{1}{2\pi\sqrt{LC}}$$

• if I plug 10 mH and 10 nF into the above I get 15.915 kHz (as calculated by the tool).

3 dB point

For a 2nd order low pass filter, the transfer function magnitude is this: -

$$|H(j\omega)| = \dfrac{1}{\sqrt{1 + \dfrac{\omega^2}{\omega_n^2}\cdot (4\zeta^2-2)+\dfrac{\omega^4}{\omega_n^4}}}$$

And, for the 3 dB frequency, the square of the denominator can be equated to 2 hence: -

$$2 = 1 + \dfrac{\omega^2}{\omega_n^2}\cdot (4\zeta^2-2)+\dfrac{\omega^4}{\omega_n^4}$$

If we let D = \$\dfrac{\omega^2}{\omega_n^2}\$ to make the math easier to follow we get: -

$$1 = D\cdot (4\zeta^2-2) + D^2$$

And solve for D we get: -

$$D = 1 - 2\zeta^2 ±2\sqrt{\zeta^4 - \zeta^2 + 0.5}$$

Or

$$\dfrac{\omega}{\omega_n} = \sqrt{1 - 2\zeta^2 ±2\sqrt{\zeta^4 - \zeta^2 + 0.5}}$$

So, if you know the Q of the circuit you can calculate \$\zeta\$ as \$\dfrac{1}{2Q}\$ and plug it into the above formula.

The example when R = 3000 produces a \$\zeta\$ of 0.1667 hence: -

$$\dfrac{\omega}{\omega_n} = \sqrt{1 - 2\times 0.1667^2 ±2\sqrt{0.1667^4 - 0.1667^2 + 0.5}}$$

$$ = \sqrt{0.9444 ± 2\sqrt{0.473}} = 1.523$$

And 1.523 multiplied by 15.915 kHz = 24.24 kHz i.e. precisely as expected.

Answer 3

The other answers said enough, already, but I'll just add, for the sake of completion, that the -3dB point is usually considered as the half-power bandwidth, so it's generally considered as the point for fc. However, this makes more sense for monotonically non-increasing passbands, such as Butterworth, Bessel, Papoulis, or Halpern. Note that these last two have ripples, but they're non-increasing, unlike Chebyshev I. Where this condition is not met, fc is usually considered at the end of the ripples (though even this is just another convention).

But you can also determine fc from the phase response. In fact, this way can be safer, since the passband is really distorted, sometimes. Just look for the point where the phase is half the total phase shift. For a 2nd order, the total phase shift is 180^o, so fc is when the phase is 90^o. You'll discover that for your case, that's around the peak. Filters are weird.