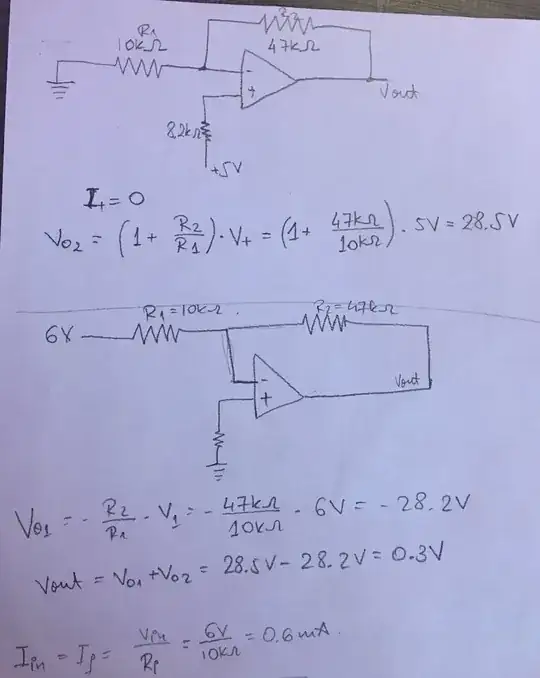
I am rewriting the answer following a point correctly raised by user287001 (merci !). If you want to apply superposition to this circuit, the only sources you can short are the 10-V on the left-side of the potentiometer and the 5-V one. Shorting the \$V_{ref}\$ node actually implies that the equivalent voltage of 6 V is generated with an extremely low resistance, negligible versus the value of \$R_i\$. Practically speaking, in this particular case, the error is small but this is not a rigorous approach hence the needed correction.
The easiest and fastest way is truly to observe that the non-inverting input is biased at 5 V (considering equal inverting and non-inverting pins biases), then the voltage across resistor \$R_i\$ is 6 V-5 V, a 1-V drop which divided by the resistance gives a 100-µA current. The same current circulates in \$R_f\$ considering the zero current going in the (-) pin. Therefore, knowing the bias at the (-) pin and the current in \$R_f\$ leads us to the output voltage:

If we now want to apply superposition to this circuit, there is no other option than determining the wiper position to know the Thévenin resistance at the \$V_{ref}\$ node. How to do this? You consider the potentiometer as two series resistance affected by a coefficient \$k\$ as shown below:
If \$k=1\$, the wiper is 100% in the low-side position and imposes 0 V on the wiper (considering the low-side terminal grounded). If \$k=0\$, the wiper is in the upper position and you read 10 V if the upper terminal is biased to 10 V. With \$k\$ varying between 0 and 1, you adjust the division ratio. By applying superposition around the equivalent circuit shown below, then you can determine where the wiper is positioned:
The, you transform the 6-V \$V_{ref}\$ node by a Thévenin equivalent circuit affected by an output resistance:

We can now alternatively short the 10-V and the 5-V sources to find the exact output voltage which is exactly 300 mV:
And finally, a quick dc-point calculation with SPICE confirms the approach is correct:
SPICE finds \$V_{out}\$ to 300 mV on the output node while the reconstructed version gives 299.999 mV.