I want to take two independent differential signals (audio line inputs with unknown properties which may be present or not), remove any common-mode noise from each of them (they could each have different common-mode noise), then sum the desired signals together. I believe I can do this all with 1 op-amp. (Actually I want to output the desired signal differentially, so I will use two of these with inverted output polarity.)
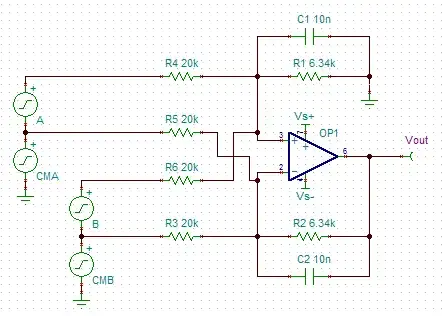
You can assume Rfeedback = Rground and all the input resistors are equal. So then I believe the output is:
$$V_\mathrm{out} = {R_\mathrm{f} \over R_\mathrm{in}} ( A + B )$$
with all the common-mode noise cancelled. Correct?
Are there any problems with this op-amp configuration?
This page calls it a "generic linear operator":
Will the CMRR be reduced by summing on the non-inverting node or anything? I did the math, and CM sources are completely cancelled out at Vout, but I feel vaguely uneasy about it. :)
The input impedance of the inverting inputs varies with the signal, as explained here, but shouldn't matter as long as it's much larger than the source impedance. The common-mode impedance is the important part, and should be the same for all input pairs.
If I weren't trying to do it all in one, I'd use two diff amps followed by a summing amp (followed by an inverter for the differential output). Does that method have any benefits over the single op-amp method?