Why will the line loss decrease when the power factor increase?

Question

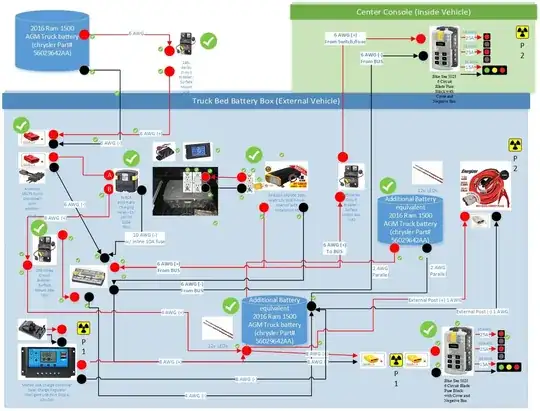
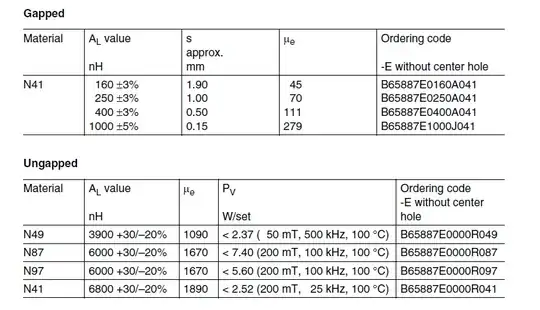
QA:

If the line loss is \$50\ kW\$ when P.F. is \$0.8\$, now if P.F. become \$0.95\$, what is the value of line loss?

Solution:

\$\frac{P_{L2}}{P_{L1}}=\frac{(cos\theta_1)^2}{(cos\theta_2)^2}=\frac{(0.8)^2}{(0.95)^2},\$ so \$P_{L2}=P_{L1} \times \frac{(0.8)^2}{(0.95)^2}=50\ kW\times \frac{(0.8)^2}{(0.95)^2}=35.45\ kW\$

I have two questions about this:

1.Why is \$\frac{P_{L2}}{P_{L1}}=\frac{(cos\theta_1)^2}{(cos\theta_2)^2}\$?

2.We can know the unit of line loss is watt\$(W)\$, that is, the line loss is a real power, not apparent power or reactive power. So if the P.F. increase from 0.8 to 0.95, that means \$\theta_1 > \theta_2\$, the real power shouldn't change, but apparent power or reactive power will decrease because of the decreasing of \$\theta\$

However, my second thinking should be wrong, because the answer of the QA does decrease with the increasing of P.F.

There is a figure about my second thinking:

Answer 1

When the load's PF is 0.8, the total current taken by that load is greater than if the load's PF was 0.95. The total current is greater because the load is taking a larger reactive current and that reactive current doesn't contribute to real power output.

However, the cable doesn't know the difference between reactive current and the current used to generate real output power and, it produces higher \$I^2R\$ losses when the PF is 0.8 compared to 0.95.

We can know the unit of line loss is Watt(W),that is, the line loss is a real power,not apparent power or reactive power.

You are confusing terms; the cable doesn't recognize power factor or phase angle, it just sees a current flow that makes \$I^2R\$ losses. Power factor (PF) is a term that applies to the load and not the cable - the cable will dissipate \$I^2R\$ losses due to any phase angle of current taken by the load.

Why is \$\dfrac{P_{L2}}{P_{L1}}=\dfrac{(cosθ1)^2}{(cosθ2)^2}\$?

Consider that the current needed to drive real power into the load was 1 amp (for example).

• At a PF of 0.8, the actual current is 1.25 amps.
• At a PF of 0.95, the actual current is 1.0526 amps.

This is because the information in the power triangle is also reflected by the current triangle: -

The current the cable carries is shown as "total current" above.

Those currents (1.25 amps and 1.0526 amps) respectively produce cable losses (per ohm) of \$1.25^2\$ and \$1.0526^2\$ respectively. So, the ratios of the cable power losses per ohm is 1.4102.

1.4102 also equals \$\dfrac{0.95^2}{0.8^2}\$. It's just another way of rearranging the numbers.

Answer 2

You have to look from the other side: Who lets PF increase? It is reactive current which is also on the line additional to the real current. And the resulting current is sqrt(ireactive^2 + ireal^2). So the resulting current increases when reactive current increases. And when reactive current increases, PF decreases after definition. Power loss is caused by resulting current, not only real current. The line doesn't know the kind of current, it only see current.

Answer 3

Well, let's first look at the definitions of the powers:

• Real power \$\text{P}\space\left[\text{W}\right]\$: $$\text{P}=\text{V}_\text{rms}\text{I}_\text{rms}\cos\left(\varphi\right)\tag1$$
• Power factor \$\text{P}.\text{F}.\$: $$\text{P}.\text{F}.=\cos\left(\varphi\right)\tag2$$

So, when we have \$\text{P}=50\cdot1000=50000\space\text{W}\$ with \$\cos\left(\varphi\right)=\frac{4}{5}\$, which is:

$$50000=\text{V}_\text{rms}\text{I}_\text{rms}\cdot\frac{4}{5}\space\Longleftrightarrow\space\text{V}_\text{rms}\text{I}_\text{rms}=5000\cdot\frac{5}{4}=6250\space\text{VA}\tag3$$

So, when \$\cos\left(\varphi\right)=\frac{19}{20}\$ we get:

$$\text{P}=6250\cdot\frac{19}{20}=\frac{11875}{2}=5937.5\space\text{W}\tag4$$