From this TI guide:
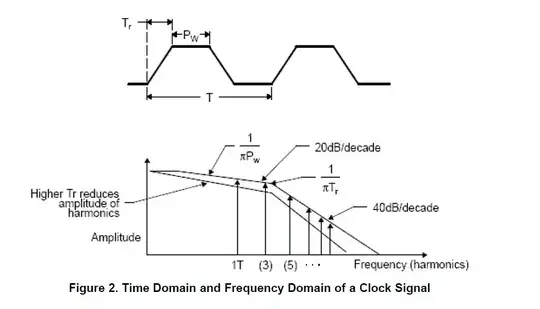
By means of the Fourier series, the trapezoid consists of a series of sine and cosine signals with different frequency and magnitude. The discrete frequency components have an envelope as is shown in the diagram of Figure 2.
Actually, there 2 envelopes are drawn; I coloured them in the graph below.
The blue envelope is the result when the Tr is increased with respect to the original signal (red envelope).
1) If the amplitude of harmonic (3) is 1/πTr what is the formula for computing the amplitude of the 5th, 7th harmonic etc.
The arrow with the text 1/πTr is not pointing at the 3rd harmonic, but at the frequency where this envelope changes from -20 dB/decade to -40 dB/decade.
The magnitudes of the harmonics are quite complex, you can find more details in this document, chapter 3.3 from college of engineering of the Michigan State University.
Using the envelope makes the relation of the magnitudes to the rise/fall time easier to understand.
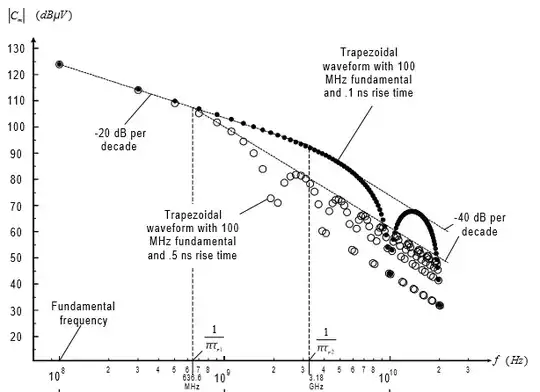
Below an example of this harmonics and their envelope.
2) What does the 1/πPw indicate? Is it the amplitude of the fundamental frequency?
I'm not sure. The arrow is pointing somewhere in the middle of the - 20 dB /decade slope.
The Michigan document I referred to uses a different (wider) definition of the pulse width.
They use \$\tau\$: at frequency \$1/\pi \tau\$ the envelope changes from 0 dB / decade to -20 dB / decade.
3) Why does the graph start off horizontally, then drop at a random point with a 20dB/decade slope until the 3rd harmonic and then shift to a 40dB/decade slope. How should I interpret this graph?
Check the document from Michican University for the details.
Note that for the blue line applies (quoted from above document):
If the frequency \$1/\pi \tau\$ occurs before the fundamental frequency, then the envelope begins with a slope of -20 dB per decade.