Non-ideal transimpedance dynamic model

Question

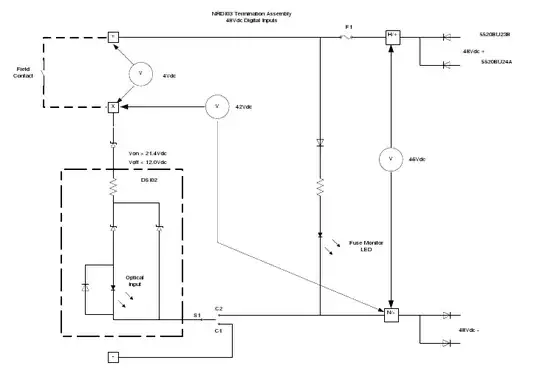
I want to determine a dynamic model (transfer function or state-space) of a non-ideal transimpedance amplifier to which is connected a photodiode at its input and a load (RC parallel).

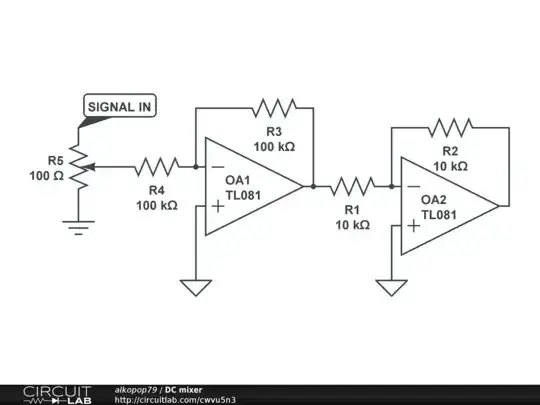
^{simulate this circuit – Schematic created using CircuitLab}

My approach to this was to first describe the circuit with the following equivalent circuit.

^{simulate this circuit}

The op-amp open-loop behavior is modeled with a second order low-pass filter and a voltage-controlled voltage source.

My goal is to find the transfer function Vout/Iin, or a set of state-space equations that would completely described this circuit dynamics. I'm a bit confused whether or not I'm allowed to used superposition principle here because of the VCVS. This thread (Superposition principle: Dependent sources treated as independent sources) provides me a great deal of information on the subject but I'm still unsure if I can safely turn off the source. Based on the previous thread, I assumed it is allowed in my case because the controlling variable of the VCVS (Vin) is not turned off (instead, Iin is).

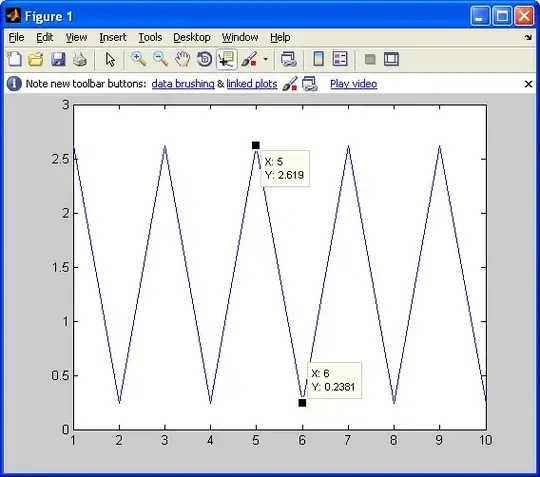
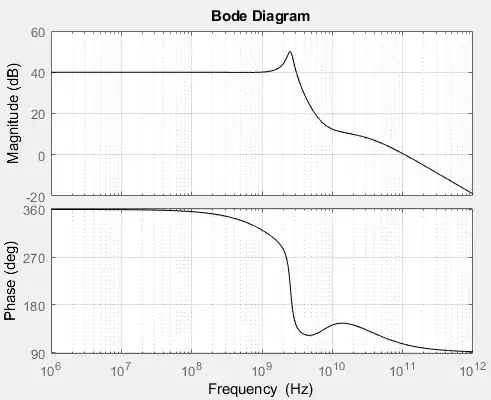
I first tried with equivalent impedances and superposition (turning off the current source, solving for Vout, turning off the VCVS, again solving for Vout and sum up the two results) but when plotting the Bode diagram on Matlab, the result was incorrect.

Then, I tried with the state-space approach but I simply didn't manage to get it work with 5 states (Vin, Vf (voltage accross feedback network) and Vout). I know that there is basically 5 energy storage components (Cin, Cf and CL and the two capacitors from the internal op-amp model) so I assumed 5 state for this circuit but maybe I'm wrong.

So my questions are:

• Is my equivalent circuit a good starting point for my initial goal?
• Am I allowed to used superposition as described above for both methods (transfer function and state-space)? If no, can someone please provides more details on why it is not allowed in my case?
• Is my assumption on the number of state correct?

Answer 1

The largest change to make in your equivalent circuit is the dependent voltage source polarity so that you have negative feedback....

^{simulate this circuit – Schematic created using CircuitLab}

Rin & Cint are the opamp's internal major pole at a very low frequency. It is assumed that this opamp has been compensated for stable unity gain. R2 & C2 may not be necessary. This opamp has 0 ohms output impedance. You might add about 100 ohms as Thevenin resistance to VCVS1 output. Not included here (it won't make much difference in this case).

Answer 2

I finally manage to get a usable model. I had to find another approach than my original thoughts on the subject to achieve my goal.

Thanks to Glen answer, I revisited the equivalent circuit that I used to derived my model. I added an output resistance of 9 Ohms and a load (RC parallel).

First, I did not use superposition principle because I'm pretty sure it is not allowed in this particular case. When turning the input current source off, the input voltage resulting get canceled out and therefore, the controlling variable of the VCVS is zero (see this thread: Superposition principle: Dependent sources treated as independent sources). I have to go deeper in my learning of superposition principle to fully understand its usability when dealing with dependent sources.

Then, I considered two cascaded transfer function, from I_in to V_in and from V_in to V_out. The global dynamics is the product of the two transfer function. This gave my very satisfying results when comparing in Spice + manufacturer model:

The transfer functions are:

$$\dfrac{V_{in}}{I_{in}} = \dfrac{Z_{in}(Z_LR_{out}+Z_fR_{out}+Z_fZ_L)}{Z_{in}Z_L(1+A(s))+Z_f(Z_L+R_{out})+R_{out}(Z_{in}+Z_L)}$$

$$\dfrac{V_{out}}{V_{in}}=\dfrac{Z_L(R_{out}-A(s)Z_f)}{Z_L(R_{out}+Z_f)+R_{out}Z_f}$$

Where A(s) is the op-amp open-loop transfer function (modeled as a second order here based on datasheet curves).

From this, I tried to derived a block diagram to highlight the feedback loop but with no success. If someone wants to try then he/she is very welcome to share their results!