I am doing math for a closed loop equation. I know the transfer function for a closed loop system is:
(Image copied from "Loop Gain and its Effect on Analog Control Systems" by Gabino Alonso and Simon Bramble)
$$ V_{out} = G \times V_{in} \tag {Eq 1} $$
$$ G = \frac {A}{1 + \beta A_0} $$
\$ A \$ - open loop gain
\$ \beta \$ - Feedback factor.
Now when I do the math like
$$ V_{out} = A(V_{in} - \beta V_{out}) \tag {Eq 2} $$
What is the initial of Vout to start with?
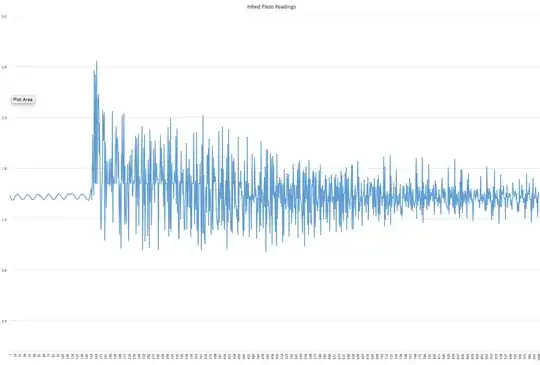
Vout numbers with 1 & 2 do not match and initial value of Vout is making a lot of difference.
Why are they not matching?
If A = 1000, B = 0.25, Vin =1, Vout =3.98;
>From Eq 1
Vout = 1000/(1+0.25*1000) = 3.98
From Eq2
Vout_initial = 0
Vout = 1000*(1-0.25 x 0) = 1000
Vout = 1000*(1-0.25 x 1000) = -249000
Vout = 1000*(1-0.25 x -249000) = 62251000
Never settles, what am I doing wrong?
If I chose A = 1; B =0.1, Eq1 and Eq2 numbers match eventually to 0.91
Vout = 1*(1-0.1 x 0) = 1
Vout = 1*(1-0.1 x 1) = 0.9
Vout = 1*(1-0.1 x 0.9) = 0.91
and
Vout = 1/(1+0.1*1) = 0.909
What's going on? What fundamentals am I missing?