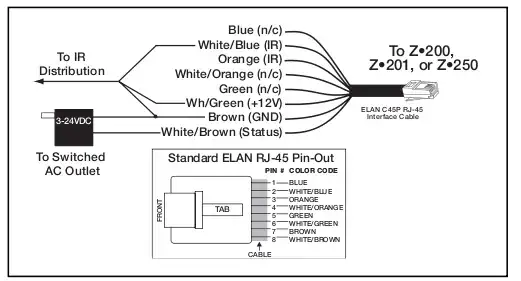
Many years ago, I found a digital circuit that squares a 4-bit input in an old textbook (perhaps 1970s or 1980s, possibly older).
(The figure below is not the original figure.
I think the figure below differs from the original in that it has been rotated 90 degrees.)
I do not have access to that textbook any more and I do not have additional details about the textbook.
Have you seen this circuit before?
If so, could you give me the name and author of the source?
I am using this figure in my teaching and I would like to properly cite the source.