Determining gain, KCL/KWL (Basics)

Question

Below is a pi model schematic of a cascaded amplifier. The goal is to find the gain with Rp as load.

So the gain would be: \$ A = \frac{V_{out}}{V_{in}}\$. So i set out to find \$V_{out}\$ in terms of \$V_{in}\$ as \$V_{out}=i_{Rp}R_p=\frac{300}{500}\beta i_{b2}R_p \$

I believe the answer is very simple, but I can't seem to express \$i_{b2}\$ in terms of \$i_{b1}\$ and thus \$V_{in}\$ because of the current \$i_1\$.

Yes, but how do I express \$i_{b2}\$ in terms of \$V_{in}\$. Current \$i_1\$ is bugging me (the node marked with an asterix). — math101, Feb 13 '20 at 16:00
Are you need a symbolic expression for a voltage gain or just a number (voltage gain)? — G36, Feb 13 '20 at 16:05
I need an expression. See, \$i_{b2}=i_1-\beta i_{b1}\$ and thus \$i_{b2}=i_1-\beta \frac{V_{in}}{r_{\pi 1}}\$ but \$ i_1\$ is unknown. — math101, Feb 13 '20 at 16:10
In that case, you need to use any circuit analysis techniques you know and solve the circuit as we do with the DC circuit, Or we can notice that the Q2 is an emitter follower and we know Zin for a voltage follower. So the IB2 current will be equal to \$\Large I_{b2} = i_{b1}*\beta * \frac{R_1}{R_1 + r_{\pi 2} + (\beta +1)*R_E||R_P}\$ See here: https://electronics.stackexchange.com/questions/476659/kvl-equations-for-this-small-signal-model/476666#476666 — G36, Feb 13 '20 at 16:19
Ah, now I get it. The resistance of the right amplifier stage could be written as \$r_{\pi 2}+(\beta + 1)*R_E||R_P\$ and then I have two branches to which the current \$I_{b2}\$ branches out to. Thank you! — math101, Feb 13 '20 at 17:43

Jan Eerland · Answer 1 · 2020-02-15T17:59:33.460

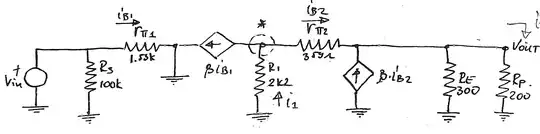
Well, we have the following circuit:

schematic

^{simulate this circuit – Schematic created using CircuitLab}

I used Mathematica to write a code using KCL and KVL. The code I came up with is the following:

FullSimplify[
 Solve[{Iin == I1 + I2, I3 == I2 + β1*I2, 
   0 == I4 + I5 + β1*I2, Ie == I5 + β2*I5, Ie == I6 + I7, 
   I1 == Ia + Iin, Ib == I3 + Ia, 0 == I4 + Ib + Ic, 
   Id == Ic + β2*I5, Id == I6 + I7, I1 == (Vin)/R1, 
   I2 == (Vin - V1)/R2, I3 == (V1)/R3, I4 == (V2)/R4, 
   I5 == (V2 - V3)/R5, I6 == (V3)/R6, I7 == (V3)/R7}, {Iin, I1, I2, 
   I3, I4, I5, I6, I7, Ia, Ib, Ic, Id, Ie, V1, V2, V3}]]

Using your values I got the following code:

FullSimplify[
 Solve[{Iin == I1 + I2, I3 == I2 + β1*I2, 
   0 == I4 + I5 + β1*I2, Ie == I5 + β2*I5, Ie == I6 + I7, 
   I1 == Ia + Iin, Ib == I3 + Ia, 0 == I4 + Ib + Ic, 
   Id == Ic + β2*I5, Id == I6 + I7, I1 == (Vin)/100000, 
   I2 == (Vin - V1)/1530, I3 == (V1)/R3, I4 == (V2)/2200, 
   I5 == (V2 - V3)/359, I6 == (V3)/300, I7 == (V3)/200}, {Iin, I1, I2,
    I3, I4, I5, I6, I7, Ia, Ib, Ic, Id, Ie, V1, V2, V3}]]

I left \$\text{R}_3\$ as it was because I need to set it equal to \$0\$ and than I will get an error message because then I will divide by \$0\$. Later I will take the limit.

Entering the code I got the following result:

{{Iin -> Vin (1/100000 + 1/(1530 + R3 + R3 β1)), 
  I1 -> Vin/100000, I2 -> Vin/(1530 + R3 + R3 β1), 
  I3 -> (Vin (1 + β1))/(1530 + R3 + R3 β1), 
  I4 -> -((Vin β1 (479 + 120 β2))/(
    3 (1530 + R3 + R3 β1) (893 + 40 β2))), 
  I5 -> -((2200 Vin β1)/(
    3 (1530 + R3 + R3 β1) (893 + 40 β2))), 
  I6 -> -((880 Vin β1 (1 + β2))/(
    3 (1530 + R3 + R3 β1) (893 + 40 β2))), 
  I7 -> -((440 Vin β1 (1 + β2))/((1530 + R3 + 
       R3 β1) (893 + 40 β2))), 
  Ia -> -(Vin/(1530 + R3 + R3 β1)), 
  Ib -> (Vin β1)/(1530 + R3 + R3 β1), 
  Ic -> -((2200 Vin β1)/(
    3 (1530 + R3 + R3 β1) (893 + 40 β2))), 
  Id -> -((2200 Vin β1 (1 + β2))/(
    3 (1530 + R3 + R3 β1) (893 + 40 β2))), 
  Ie -> -((2200 Vin β1 (1 + β2))/(
    3 (1530 + R3 + R3 β1) (893 + 40 β2))), 
  V1 -> (R3 Vin (1 + β1))/(1530 + R3 + R3 β1), 
  V2 -> -((2200 Vin β1 (479 + 120 β2))/(
    3 (1530 + R3 + R3 β1) (893 + 40 β2))), 
  V3 -> -((88000 Vin β1 (1 + β2))/((1530 + R3 + 
       R3 β1) (893 + 40 β2)))}}

Now using your gain formula we will end up with:

$$\text{G}:=\frac{\text{V}_3}{\text{V}_\text{in}}=\lim_{\text{R}_3\to0}-\frac{88000\beta_1\left(1+\beta_2\right)}{\left(1530+\text{R}_3\left(1+\beta_1\right)\right)\left(893+40\beta_2\right)}=$$ $$-\frac{8800\beta_1\left(1+\beta_2\right)}{153\left(893+40\beta_2\right)}\tag1$$

lol, I could write down the voltage gain expression by inspection. So there is no need to write down all these equations. — G36, Feb 15 '20 at 16:49
@G36 Well, impressive that you're able to do that, not everyone is 'that' advanced. — Jan Eerland, Feb 15 '20 at 16:50
Yes, but "your method" is inefficient, too many equations. Why you do not use more efficient method? — G36, Feb 15 '20 at 16:54
@G36 If you want to know all the voltages and currents, I think my method is the way to go. Yes indeed if you only want the voltage at the output you can use the 'easy' method. — Jan Eerland, Feb 15 '20 at 16:56
But are you aware that the "alpha" in BJT's is a current gain of a common-base amplifier? "alpha" \$\alpha = \frac{I_C}{I_E} =\frac{I_C}{I_B +I_C}= \frac{\beta \cdot I_B}{I_B +\beta \cdot I_B}= \frac{\beta}{\beta + 1}\$ and "beta" \$\beta = \frac{I_C}{I_B}\$ — G36, Feb 15 '20 at 17:02
R5 = 359R and you should use \$\beta1\$ and \$\beta2\$, not Alpha to avoid confusion. — G36, Feb 15 '20 at 17:11
Also, can you explain why an additional R3 resistor is needed? — G36, Feb 15 '20 at 17:14

Determining gain, KCL/KWL (Basics)

1 Answers1