5

Still having a problem with measured value of Q factor of parallel LC circuit. My measurememt setup looks like on the picture below. I use Function generator SFG-1003 and Oscilloscope Rohde-Schwarz RTB2002. enter image description here

My LC circuit consists of:

L= 33,4 uH R= 0.3 Ω C=32,63 nF

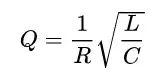
Using equation, we get Q factor of 106. enter image description here

I also simulated my LC circuit and using equation

enter image description here

getting the Q factor of 101.

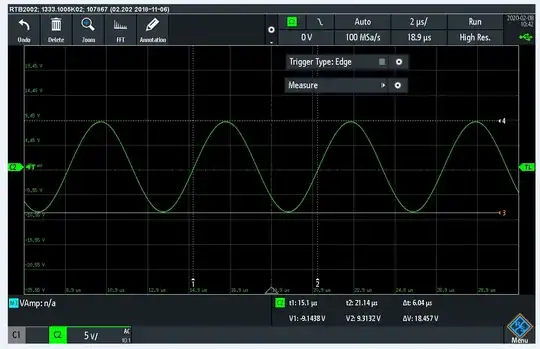
enter image description here

But problem is with my measurements. I followed this ring down tutorial to get a Q factor: https://www.giangrandi.ch/electronics/ringdownq/ringdownq.shtml

but my results giving me the Q factor almost nothing. I also tried to get on the resonant frequency with my signal generator, and did a measurements of bandwidth (0.707 multiplied by amplitude) but it is the same as with ring down method. I attached my results.

enter image description here enter image description here enter image description here

In my opinion, the problem is just with measurements setup, but I do not know how to use a function generator for LC circuit, which has variable impedance. In parallel LC circuit the impedance is pretty high in resonance, so how can I measure Q factor of LC circuit correctly? One idea came to my mind to use an operational amplifier to solve a problem with impedance matching. Or the problem is something else?

Thank you

!!!EDIT!!!

I edited my circuit. Put another coil on the primary side with generator. Then I placed secondary coil with capacitor (where I measure Q factor) nearby, to have loosely coupled system (10 cm). Primary coil inductance is 3.5uH and secondary coil inductance is 187uH. I did few measurements with different values of capacitor to get resonant frequencies (60kHz - 300 kHz).

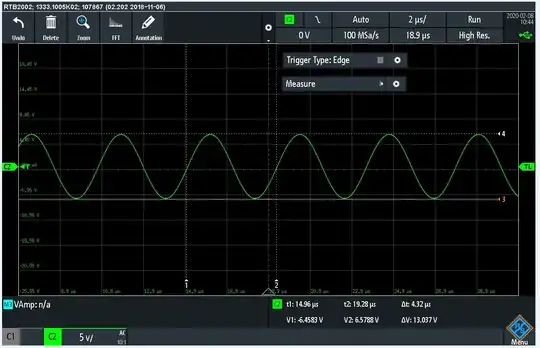
With this measurement setup I did the same experiments (ring down method + ratio of resonant frequency and bandwidth) I got results attached below: enter image description here

Used capacitors [32nF 13.3nF 5.6nF 1.5nF] As you can see measured values of Q factor and then calculated values of Q factor using ONLY DC resistance of coil(2,1ohm). With increasing resonant frequency also difference between calculated and measured values increase. This is probably evidence of AC resistance (caused by skin effect, proximity effect, etc.)

Coil with 187uH, length=6m, Diameter=0.3mm, copper wire, 3 layers.

I did another measurement setup as shown in the picture below. With L=187uH and C=1.5nF. It gives resonant frequency around 300kHz. Signal generator was tuned to 300 kHz. And I measured VPP2 and VPP1.

enter image description here

When reactance of coil and capacitor is equal in magnitude then parallel LC circuit in resonance is purely resistive. So when I see on my oscilloscope VPP2=2*VPP1 (2* because of impedance matching), then I get parallel resistance of LC circuit Rp.

My resistor was adjusted to 9.9kOhm. Using equation (parallel RLC circuit) Q=R*sqrt(C/L), it gives Q = 28 (measured value using bandwidth method was Q=30)

In my opinion coils were loosely coupled so damping effect of the primary coil was not so significant. Do you think that AC resistance of LC circuit can be 5 times higher than DC resistance in frequencies around 300kHz?

Kols
  • 63
  • 1
  • 5
  • 1
    probably not your problem but the sig generator you are using has quite slow rise time - <100ns says the data sheet. If you used some high speed CMOS drivers you should be able to get <10ns and also reduce source impedance a bit. https://www.gwinstek.com/en-global/products/downloadSeriesDownNew/5826/490 – danmcb Feb 17 '20 at 08:29
  • Definitely, that is true. rising edge is not perfectly straight and time constant of rising edge of signal generator is pretty high. That is also another effect on the damping evidence. Thank you – Kols Feb 17 '20 at 20:27

4 Answers4

8

My LC circuit consists of:

L= 33,4 uH R= 0.3 Ω C=32,63 nF

Not quite true; there is also the 50 ohm impedance of the signal generator parallel loading the LC. You would need to drive this circuit differently i.e. with a current source if you wanted to measure Q factor: -

enter image description here

Resonant frequency is at 152.524 kHz and the 3 dB point is at 153.241 kHz. The upper and lower 3 dB bandwidth is therefore 1.434 kHz and the Q is centre frequency divided by bandwidth is: -

$$\dfrac{152.524}{1.434} = 106.36$$

In my opinion, the problem is just with measurements setup, but I do not know how to use a function generator for LC circuit, which has variable impedance.

Correct.

Andy aka
  • 434,556
  • 28
  • 351
  • 777
  • Thank you for your advice. Today I tried some experiments with DC voltage source and transistor to deliver more power to do system. So I connect my L-C circuit to the source of transistor and I got correct Q factor value but with frequency 10 times higher. Anyway I will do some experiments with current source. – Kols Feb 09 '20 at 20:21
  • What frequency did you measure at and what frequency did you calculate it would resonate at? – Andy aka Feb 09 '20 at 20:25
  • Measured frequncy: 1.6MHz Measured Q factor: 59 Calculated frequency: 157kHz Calculated Q factor: 66.2 – Kols Feb 09 '20 at 20:32
  • Well maybe you had an incorrect inductance value because it should be around 150 kHz. I’d concentrate on resolving this before moving on. – Andy aka Feb 09 '20 at 21:02
  • Thank you, but do not think problem would be inductunce value, according my previous values, calculated resonant frequency is 152kHz and measured resonant frequency is aprox 160 kHz. difference is less than 10 percent. Impact on calculated value of Q factor would be minimal. And I did the same experiment with plenty of coils and all of them are the same. As I said, problem probably is with measurement setup... – Kols Feb 09 '20 at 21:27
  • Well, if you’re done with this question, please consider formally accepting the answer that is most appropriate. – Andy aka Feb 09 '20 at 22:07
  • Did you get to the bottom of this problem @Kols – Andy aka Apr 20 '20 at 15:19
  • I followed all measurements setup I posted above and all of them gave me the same result of Q factor.. seems that damping constant of LC is high...important is that Q factor of LC circuit is limited by Q factor of coil.. – Kols Apr 20 '20 at 15:26
  • But, your basic question of using the signal generator across the coil was addressed in my answer yes? – Andy aka Apr 20 '20 at 15:37
  • Yes. You can not use signal generator with 50ohms impedance directly to LC circuit if you want to measure Q factor. Then Q factor is affected by input impedance. – Kols Apr 20 '20 at 15:40
  • Well, it looks like you have extended your question quite a bit since first raising it but, if you feel the original underlying problem has been addressed you should consider formally choosing the right answer or leaving an answer of your own that explains what the solution was. – Andy aka Apr 20 '20 at 15:49
3

Three things to consider

  1. Component tolerances.The values you have selected might not physically be those values. There can easily be +-10%
  2. The inductor will have resistance to help dampen out the oscillation
  3. The ring-down method requires you to excite the circuit at its resonance frequency. Your L-C has a resonance at 1.6MHz while you have excited it at ~40KHz
  • 1
    Thank you for your comment, DC resistance of coil is part of my circuit R=0.3 ohm and I think in relatively low frequencies (1-100kHz) skin effect does not affect so much to significantly change calculated resistance. How can I see damping effect if I get on the resonant frequency? My L-C circuit has resonant around 160kHz and excite circuit using 1kHz signal gives me view on the logarithmic decrement of damped L-C circuit, cant be seen in resonant frequency. – Kols Feb 09 '20 at 20:11
  • no, you excite the circuit at some frequency much less than fo - the 40kHz is fine. The edge is what makes the circuit ring, the frequency of the square wave is just to make it easy to see on an analogue scope. – danmcb Feb 17 '20 at 08:31
  • @danmcb do not know, what you mean. I excited circuit with square wave with frequency 1kHz. Exactly because of reason to see it clearly on oscilloscope. – Kols Feb 17 '20 at 20:22
  • and here in lies WHY I stated what I did. The ring-down method explicitly states you must excite the LRC at its resonance "first you have to "shake" the resonator someway to make it oscillate at its natural frequency." The paper is hitting it with a squarewave and thus will contain the harmonics. The OP however has note stated he is exciting with a squarewave, in fact fig3 is a sinewave. IF the OP is hitting with a squarewave then fine –  Feb 17 '20 at 21:57
  • @Kols my comment is directed at point 3 of JonRB's answer – danmcb Feb 18 '20 at 08:43
  • @JonRB OK that is indeed a good point. – danmcb Feb 18 '20 at 08:44
2

0,3 Ohm resistance maybe isn't true at higher frequencies due the skin effect. But the connection to the signal generator should be kept very loose to prevent its 50 Ohm to affect the result. Insert a capacitor in series with the signal generator. Try one which has 100 x bigger reactance than the LC parts in the resonant circuit at the interesting frequency range. I guess you can use about 150pF.

You can try to disconnect one end of the 36.2nF capacitor, charge the cap with DC and then connect it again with mercury switch or other non-bouncing method. The voltage of the LC circuit (=decaying sine) can be stored to an oscilloscope. You can decide the actual resonant freq and Q from the decaying sine.

ADD after getting the wire thickness and length of the coil: It's not skin effect who pulls the Q down. Assuming the measurement is properly performed there's left "other losses". I guess your coil is too near some lossy material. Try to keep it far away everything including paper, wood, unknown plastics etc. Let it hang in the air.

  • Thank you for your advice. I tried with capacitor 22pF and distance between LC circuit and generator probes more than 5 cm... measured Q factor less then 100... much lower than calculated.. – Kols Feb 09 '20 at 19:56
  • Very loose inductive coupling does the same as coupling with a small capacitor. I guess your coil has much more resistance than 300mOhm. What's the resistance of your coil at 152kHz? (= wire material resistivity, how thick wire, the length of the wire and the skin effect all taken into the account) –  Feb 09 '20 at 20:38
  • Measured DC resistance of coil is R=0.3Ohm. Calculated AC resistance (157kHz, D=0.67mm, L=3) is around 0.145Ohm. Q factor calculated is still much higher, than measured, more than 10 times. – Kols Feb 09 '20 at 20:58
  • I tried that with plenty of coils but always in range of resonant frequency (50kHz - 150kHz). still the same problem. – Kols Feb 09 '20 at 21:01
  • L=3? is that wire length. What is the unit? –  Feb 09 '20 at 21:05
  • sorry 3 metres.. aproximately, between 2.5-3m – Kols Feb 09 '20 at 21:11
  • OK the skin effect isn't the cause. It was a bad guess. –  Feb 09 '20 at 21:34
  • The same thing: https://www.youtube.com/watch?v=tjbK4LsOQRk&t=1s – Kols Feb 09 '20 at 21:35
  • Thank you very much, you were probably right with ''other looses''. Not caused by items nearby, but probably another looses like skin effect, proximity effect, etc. I updated my results and evidence of resistance increasing is clear. Just not able to classify these looses, I do not believe that skin effect would increase resistance so significantly. – Kols Feb 17 '20 at 20:20
0

There are 3 separate issues. First, the 50Ohm generator resistor that has been mentioned. Second you are assessing the value of series Q and measuring parallel Q. Lastly, if the generator edge speed is slower than 0.35/FR this will also add damping effect.

You might see my article here, as it is a similar problem

https://www.signalintegrityjournal.com/blogs/8-for-good-measure/post/1288-measuring-a-scope-probe-requires-two-oscilloscope-channels-and-a-very-flat-signal-source

STEVE M SANDLER
  • 11
  • 1
  • Thank you for your comment, yes I am trying to solve the impedance problem. Why do you think I should use formula for parallel? Wiki says: In a parallel LC circuit where the main loss is the resistance of the inductor, R, in series with the inductance, L, Q is as in the series circuit. This is a common circumstance for resonators, where limiting the resistance of the inductor to improve Q and narrow the bandwidth is the desired result. Moreover LtSpice has a simulation which also corresponds with formula for series circuit. – Kols Feb 09 '20 at 20:16