5

In the following diagram:

enter image description here

The current is 1 mA from:

V = IR
R = 1 / 1000 = 1 mA

However, when I add in an LED with forward voltage 1V:

enter image description here

Why does adding in the LED drop the current as well? Does an LED have resistance as well? (I thought an LED only causes a voltage drop but doesn't have resistance). How does that work?

David542
  • 669
  • 2
  • 7
  • 15
  • 7
    `LED only causes a voltage drop` ... what do you think that happens to the voltage drop across the resistor then? – jsotola Feb 02 '20 at 00:34
  • @jsotola Actually, I would expect the node showing 767 mV would be 1V (as the forward voltage of the LED is 1 V). – Michel Keijzers Feb 02 '20 at 00:41
  • David, that's a [level 2 or above](https://electronics.stackexchange.com/a/478757/38098) question, because the voltage is low and you are including substantial resistance, too. – jonk Feb 02 '20 at 00:52
  • David, go into Falstad with the circuit you used and let us know what the LED model parameters are. (These will be Level 2 model parameters: saturation current, emission coefficient, etc.) If we grab those, the simulation can be explained. – jonk Feb 02 '20 at 02:14

4 Answers4

9

A bog-standard red LED has a forward drop of about 2 volts at 20 mA so yes, it has a significant impact in what current might flow when the supply voltage is only a few volts: -

enter image description here

So, with 2 volts across it and 20 mA flowing, the perceived resistance is 100 ohms. With 1.9 volts across it, the current is only 5 mA and the perceived resistance has risen to 380 ohms. At only 1.8 volts, the current might be 1 mA and this means it looks like 1800 ohms. Do you see the issue?

For instance, if your supply voltage was only 1 volt then forget it because it won’t overcome the innate forward voltage of the LED and, barely nano amps will flow.

Other LED colours can have significantly higher forward voltages so, what you are trying to achieve depends on the LED type.

So, like the game rock, paper and scissors, the LED dictates current flow at low voltages but, at higher voltages, the series resistor wins.

Andy aka
  • 434,556
  • 28
  • 351
  • 777
  • But one (simple) *model* of a diode (LED in this case) is a (current-independent) fixed voltage drop with zero resistance (an ideal [voltage source](https://en.wikipedia.org/wiki/Voltage_source)). A more accurate model comes with more complexity. It depends on what it is going to be used for. The component-to-component variation may also be significant, e.g. [2.8 V - 3.8 V](http://lednique.com/current-voltage-relationships/variations-vf-binning/). – Peter Mortensen Feb 02 '20 at 21:15
  • 1
    @PeterMortensen I’m unsure what you might be trying to say here and how it might have relevance to the question or my answer? – Andy aka Feb 02 '20 at 21:34
6

Please do following things.

  1. Change the supply voltage to 5V.

  2. Calculate the current through the resistor considering the LED as a voltage source of voltage equals to froward vorlage drop of the LED (polarity will be reverse).

  3. The currents wil then match. The reduction in current is due to reduction in voltage across the resistor with and without the LED.

Note that, the LEDs will have very small currents until the applied voltage across the LED is less than their forward Voltage.

Once the applied voltage crosses the LED forward Voltage, the current will be very high (the series resistor will define the current)

enter image description here

User323693
  • 9,151
  • 4
  • 21
  • 50
2

A first-order approximation of a red/yellow LED is Vf = 1.85 V + If*Rs for If > 15% rated current, while Rs has a wide tolerance deviation that results in Vf tolerances at rated If.

Thus if Vf = 2 V @20 mA, Rs = 0.15 V/20 mA = 7.5 ohms.

Below this threshold the diode voltage had a logarithmic relation with If.

Peter Mortensen
  • 1,676
  • 3
  • 17
  • 23
Tony Stewart EE75
  • 1
  • 3
  • 54
  • 182
2

Why does adding in the LED drop the current as well? Does an LED have resistance as well? (I thought an LED only causes a voltage drop but doesn't have resistance).

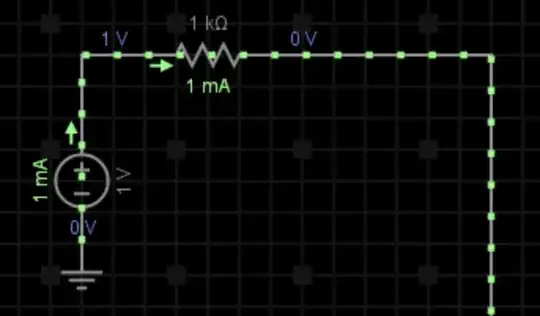
An LED does have resistance in that it resists current flow. If it didn't there would be no voltage drop across it and, since P = VI, with V = 0 it could not consume any power or produce any light. We don't treat it the same as a resistor though because the relationship between voltage across an LED and current through it is not linear. (Ohm's brilliance was showing that there is a linear relationship for a true resistor.)

Hopefully the following will help.

LEDs do not have a linear relationship between current and voltage so they cannot be modeled as simply as a resistor using Ohm’s Law, V=IR. We can, however, make a simplification and model them over a range of currents as a combination of a resistor and a voltage source.

enter image description here

Figure 1. An LED can be approximated as a resistor with a fixed voltage source.

If we look at a typical LED IV curve we can see that it is approximately linear over much of its useful range. This allows us to model the LED as a resistor and voltage source.

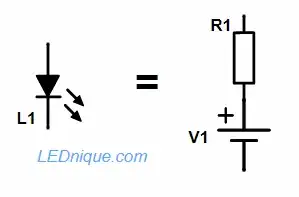
enter image description here

Figure 2. LED equivalent circuit model.

In Figure 1 the grey line is reasonably close to the LED curve from 20 mA to 100 mA. We can work out the resistance that this represents from Ohm’s law V=IR but in this case we will look at the change in voltage and current in the area of interes.

$$R = \frac {ΔV}{ΔI} = \frac {3.5–2.0}{100m–0} = \frac {1.5}{100m} = 15 \ Ω $$

We can also see that the line crosses the X-axis at Vf = 2.0 V. Our equivalent circuit for this region of interest is (referring to Figure 2) R1 = 15 Ω and V1 = 2.0 V.

All images and text from my article Resistance of an LED. There is a little more in the article.

Transistor
  • 168,990
  • 12
  • 186
  • 385