I need to derive an expression for Zin = Vin/Iin, which is the equivalent impedance looking into the input. I'm not sure how to approach this. I know that no current flows into the op amps and it doesn't look like this circuit can be separated.
Thanks
simulate this circuit – Schematic created using CircuitLab
Your circuit is the well-known GIC structure invented by A. Antoniou already in 1969. This a very versatile block for realizing "active inductors" (your example) and "Frequency dependent negative resistances (FDNR)"
There is a simple trick for easily finding the input impedance:
Assuming that both opamps are ideal, the diff. voltage across the input terminals may be set to zero. Now - because both inv. terminals are connected to each other we also can say that both non-inverting terminals have the same potential (voltage versus ground). Therefore, without modifying the properties of the whole circuit, we are allowed to swap both non-inv. terminals.
As a result (perhaps it is good to make a re-drawing) you will see that both opamp circuitries are separated (connected in series). Furthermore, you will see that the whole block consists of two NICs (Negative Impedance Converter) in series where the normally grounded resistor of the first NIC is replaced by a second NIC.
When you have the input impedance of such an NIC (simply to derive, can be found in each relevant textbook), it is no problem to find the wanted input impedance of the whole circuit.
Remark: The last structure (Two NIC in series) can be used as a GIC as well (because it has the same properties as the shown circuit - however, for ideal opamps only!). Due to the cross-wise connections, the Antoniou topology has the advantage that opamp non-idealities (finite and frequency-dependent gain) are compendsated up to a certain degree.
2nd remark: I forgot to mention that - after swapping the non-inv. input nodes - we have two different NIC circuits in series (one is short-circuit stable and the other one is open-circuit stable). Only this combination ensures stability of the whole circuit.
If Leonardo or Gauss lived today they maybe could write the right formula in the fly (assuming they saw the problem interesting). The rest of us must bite the bullet and write a bunch of equations and eliminate the node voltage variables until we have Vin, Va, X and Y where X and Y are the voltage gain factors of the opamps.
The equations in this case are
elementary voltage division equations for opamp input voltages and
opamp output voltages presented as input voltage difference multiplied by the voltage gain.
The method to start from circuit equations is general, it's not limited to this case only.
The next step is to find the limit equation between Vin and Va when X and Y approach infinity. If the limit exists, we'll have Va=F * Vin where factor F contains component values R1, R2, R3, R4 and sC1. The s is the Laplace transform s, it is taken into the account by equation Vd= Vc(R4/(R4+1/sC1)).
Then we'll write Va = F * Vin = Vin - Iin * R1. It reduces to Vin/In = R1/(1-F) and that's your Zin.
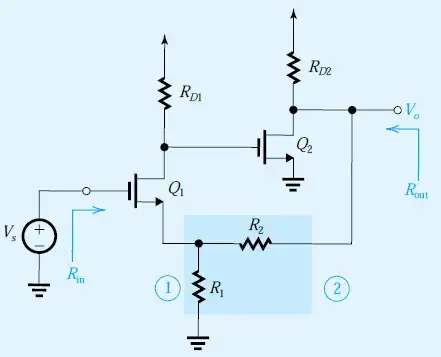
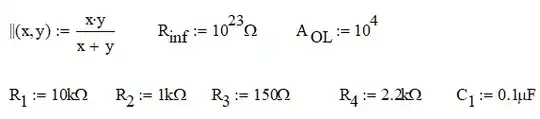This type of configuration is always intimidating considering the weird op-amps arrangement. To look at the impedance, I prefer using the fast analytical circuits techniques or FACTs described in the book I wrote. To determine an impedance, you can install a test generator \$I_T\$ producing a voltage \$V_T\$ across its terminals. the ratio \$\frac{V_T}{I_T}\$ is the impedance you want.
First, I check the basic dc resistance \$R_0\$ with the complete circuit and a re-drawn version implying non-ideal op-amps. Running an operating point SPICE simulation tells me if I'm good to go. Bias points say yes:
To determine the dc input resistance \$R_0\$, open the capacitor and determine \$R_0=\frac{V_T}{I_T}\$ in this mode:
With a few equations, you confirm the dc operating points:
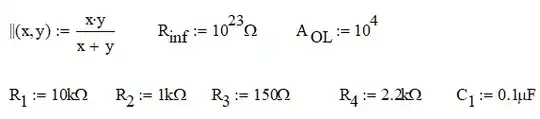
In the above lines, you see that with an open-loop gain approaching infinity, the dc resistance is 0 \$\Omega\$.
The next step is to determine the pole position. Turn the excitation off (zero the current source) and install the test generator across the capacitor:
If you do the maths ok, you find:
With a gain approaching infinity, the pole is infinite too. Now, for the zero, you have to null the response. The response is \$V_T\$ across the current source in the first sketch. When nulled, we have a degenerate case and the current source can be replaced by a short circuit. Determine the resistance seen from the capacitor connecting terminals in this mode and you have the zero position:
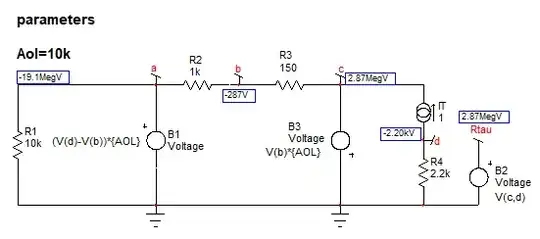
Again, if the maths are ok you have:
This is it, we have the complete impedance transfer function expressed as:
\$Z_{in}=R_0\frac{1+\frac{s}{\omega_z}}{1+\frac{s}{\omega_p}}\$. From this formula, considering an inductive impedance equal to \$Z_L=R_0+sL_{eq}\$, we can express the emulated inductance equal to: \$L_{eq}=\frac{R_0}{\omega_z}\$:
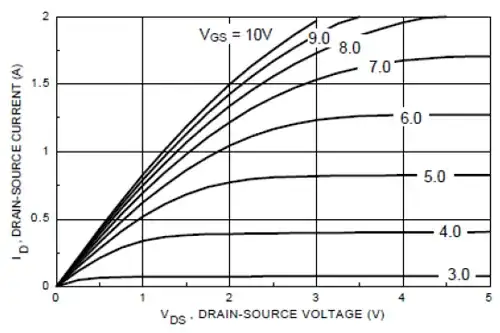
With the component values I used, the inductance is 330 µH with a 1.5-\$\Omega\$ dc resistance in series. If the op-amps are perfect, you have a purely inductive component. The input impedance plot with a 10k open-loop gain is there:
Here the FACTs let you determine the complete transfer function without analyzing the circuit: determine the time constants in two conditions (zeroed excitation and nulled response) and you have your transfer function including the op-amp open-loop gain effects. What is cool is that you can use SPICE to check your calculations via a .OP simulation and make sure the bias points exactly match the Mathcad sheet. This is an excellent way to progress in the process without making mistakes.
People are making far too much of this. the input current will ALWAYS be \$I_{in}=\frac{V_{in}- V_A}{R_1}\$, and as you said \$Z_{in}=\frac{V_{in}}{I_{in}}\$. Note that \$V_A\$ is simply the output of the circuit
Now, let's look at what we know given the "rules" for op-amps in negative feedback, the input terminals will be at equal voltages. This means \$V_B=V_{in}=V_D\$!!!
Since you now know \$V_D\$, you know the current through \$R_4\$, which will be the same as the current through \$C_1\$. All this is used to calculate \$V_C\$.
Now, you can calculate the current through \$R_3\$, and the current through \$R_2\$ will be the same, giving you \$V_A\$.
Sure, lot's of steps and tedium, but no rocket science.
A step-by-step derivation of input impedace for someone who needs it.
simulate this circuit – Schematic created using CircuitLab
