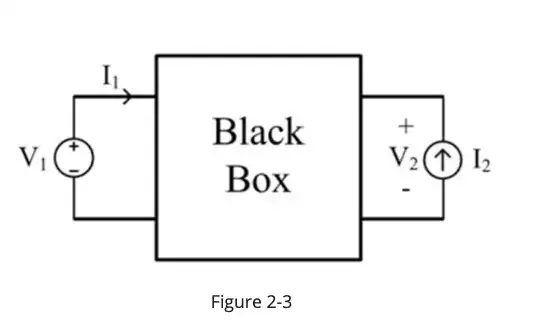
We are given a black box that contains only linear circuit elements and a pair of ports. We conduct the following two experiments with this black box.
With the right port open, we applied V1 = 2V to the left port and measured I1 = 4mA and V2 = 8V.
With the left port shorted, we applied I2 = -10 mA to the right port and measured I1 = 5mA and V2 = -10V.
Now we connect a current source to the right port and a voltage source to the left port. I1 = 8mA and V2 = 4V now. Find I2 and V1, in mA and V each.
I don't get this. Since we have analyzed the circuit separately for each source, adding them should give me the final values of I1, V2, I2, V1 etc. However, that's not quite true—from cases 1 and 2, I should have I1 = 4 + 5 = 9 mA, but it's 8mA. Hence, I thought that the black box consumes 1mA; hence I2 = 0 + (-10) - 1 = -11 mA. Similarly, V2 = 4V even though adding the V2 from first two cases gives -2; hence, the black box provides an additional 6V, and so V1 = 2 + 0 + 6 = 8V. However, this approach is wrong.
How might I solve this?