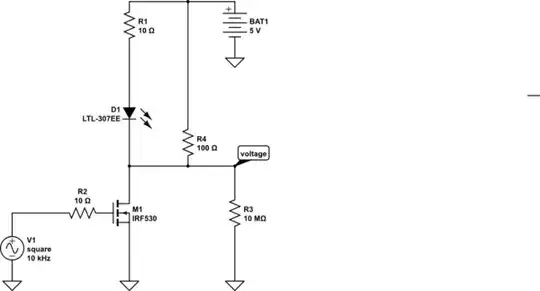
So in this circuit, initially the current and voltage is 0. At t = 0 the voltage snaps to V.
Now my analysis is: According to Lenz Law the voltage developed will be in the direction as specified in red markings in the image because a back emf will be developed. So the KVL equation would be:
\$-v_S + i_L R - v_L = 0\$
Applying Faraday's Law we get:
\$-v_S + i_L R - L \frac{di_L}{dt} = 0\$
Now I have taken \$v_L\$ to be the magnitude of the voltage, because since we indicated the direction in the circuit.
But the textbook has this equation, obviously I am wrong but I cannot see where my reasoning is wrong.