What is the price of increasing the QAM number?

Question

In a QAM modulation scheme, you have a certain number of possible states which have different amplitudes/phases (like 4-QAM, 16-QAM). If you increase the number, for example switch from 16-QAM to 64-QAM, you will get a higher bit rate. But what is the price you pay for this bit rate increase?

Answer 1

What happens when you increase the amount of distinct states in QAM is you get a higher BER (bit error rate).

source

To achieve the higher data rate with the same BER, you need to use error correction coding. You see, the BER rises, but your ability to correct the errors increases at a greater pace, as Shannon discovered.

Answer 2

what is the price you pay for this bit rate increase?

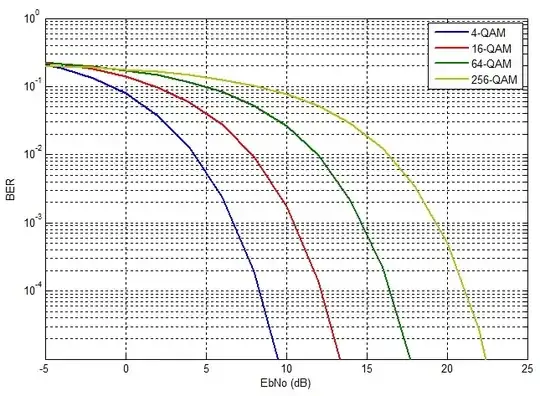
The price you pay according to Shannon-Hartley Theorem is SNR. You need a much higher SNR (S/N) or Eb/No ratio to compress more Bits/baud.

\$~~~~@~BER=10^{-5}\$

  Eb/No  QAM [dB]
  ----   ---
     4   9.5
    16  13.0 (+3.5)
    64  17.5 (+4.5)
   256  22.5 (+5.0)

For Gaussian Noise you can extrapolate in dB/decade of BER.

The problem with telephone 56k modems in the 90's was not the DSP equalization of phase frequency response in end-to end with very high SNR, but rather the software modems could only compensate for 1 exchange conversion delay return loss. Hardware DSP type modems had more power to equalize more than one return loss echo in the training initialization to obtain 64kBd in 4kHz audio BW but due to FCC interference on all phone lines had to limit the bit rates to 56k.

Today cable and phone line modems split up the bands into sub-bands so each can be DSP equalized flat amplitude and phase within a small sub-band then concatenate all these modems into 1 aggregate high speed modem like mine 250Mbps.