Such fundamental questions have always made me think about the philosophy of negative feedback op-amp circuits looking for where it all starts. This is the kind of fancy story I wrote these days, in which I show the evolution of these circuits. For the purposes of intuitive understanding, I have used descriptive and figurative names of the devices under consideration but have shown their relationship to conventional names.
Building scenario
I have built the circuit solutions step by step and examined them using CircuitLab. To keep the schematics simple and clear, I have not used named nodes and ordinary DC simulation but a live DC simulation. So hover your mouse over elements and their terminals to see the quantity values.
STEP 1: Zero voltage follower undisturbed
As a result of much observations and reflection, I have come to the conclusion that the initial negative feedback circuit is a voltage follower with zero input voltage. To make this "circuit", we just need to connect the output of an inverting amplifier to its input.
simulate this circuit – Schematic created using CircuitLab
There is hardly a simpler "circuit" than this, because it consists of only an amplifier, which may not even be an op-amp with a differential input but a humble amplifier with a single-ended input (if there was one in the CircuitLab library, I would use it). And what is most interesting about this most elementary implementation is that no high gain amplifier is needed. If you open the op-amp properties in CircuitLab, and start setting the gain lower and lower, you will see that the circuit works (produces zero voltage) even at a gain of 1. This is because there is no disturbance and the op-amp does its job effortlessly. It watches the input intently, and every time something tries to change the zero voltage, it changes its output voltage in the opposite direction (actually the two voltages are the same).
STEP 2: Zero voltage follower disturbed by a floating voltage source
It is a bit hard to imagine what we can use such an output-only circuit (zero voltage source) for... maybe as a virtual ground. So let's try to find an input where to apply an input voltage. And here, as above, with much thought I eventually realized that this actually means finding an entry point where we can perturb the op-amp... disturb its "peace":-) Since it has set itself the goal of maintaining zero voltage, any attempt to change this voltage represents a disturbance to it, which it tries to compensate for. This forces it to change its output voltage in proportion to the disturbance. For example, we can insert the "disturbing" input voltage between the input and the output.
simulate this circuit
At the first moment, the op-amp fails to respond and its output voltage remains zero. Because we have connected the positive terminal of the input source to the output, the op-amp input voltage (at the inverting input) becomes negative. So the op amp begins to vary its output voltage in a positive direction until the ratio of its output to input voltage equals its open-loop gain. Open the op-amp properties in CircuitLab and set various gains from one to several hundred thousand (1 ÷ 300,00 or more); then hover your mouse over the op-amp input and output.
As you can see, as the gain increases the op-amp keeps the ratio between its output and (differential) input voltage equal to its open-loop gain. The op-amp input voltage remains negligibly small and the output voltage is almost equal to the circuit input voltage Vin.
STEP 3: Zero voltage follower disturbed by a grounded voltage source
The voltage follower we "invented" is great, but there is a problem - the input voltage source is "floating" (not connected to ground). A simple rule of thumb is that out of three devices connected in series, at least one must be floating. Now it is the turn of the op-amp input - ie. to ground the input source we need a differential input. Ah... that is why it was invented back in the day!
simulate this circuit
As above, at the first moment, the op-amp fails to respond and its output voltage remains zero. Because the op-amp input voltage (at the non-inverting input) becomes positive, the op amp begins to vary its output voltage in a positive direction until the ratio of its output to (differential) input voltage equals its open-loop gain.
Now set various gains and hover your mouse over the op-amp input and output. As you can expect, the op-amp input voltage remains negligibly small and the output voltage is almost equal to the circuit input voltage Vin.
Then run a DC sweep simulation varying the op-amp open gain. For example, in the graph below, it only changes from one to 100 and yet the op-amp input voltage drops to 10 mV. You can only imagine what it will be like when amplified 300 thousand times!
STEP 4: Zero voltage follower disturbed by a current source
There is a solution that combines the advantages of the above two - to disturb the voltage follower through a current source; then both the source is grounded and the op-amp input is single-ended. For this purpose, we can try to change the op-amp input voltage (disturb the op-amp) by the input voltage source Vin through a resistor R1. Figuratively speaking, the input source is trying to "pull up" the op-amp inverting input through a resistor R1 but the op-amp output does not let it by "pulling down" to ground the inverting input through a conductor with zero resistance (a piece of wire). As a result, nothing happens.
simulate this circuit
To help the input source, we can make it difficult for the op-amp by including a resistor R2 between its output and the inverting input. Thus, the two sources are placed under the same conditions. As in the game "tag of war", they "pull" the common point with the same "force" but in different directions - the input voltage source Vin "pulls up" through R1, and the op-amp output "pulls down" via R2.
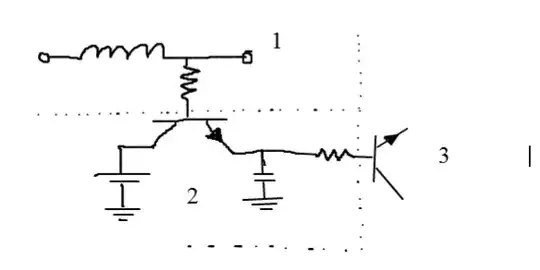
simulate this circuit
STEP 5: Potentiometric inverting amplifier
We can make the inverting circuit more attractive if we replace the two discrete resistors R1 and R2 above with a linear potentiometer P.
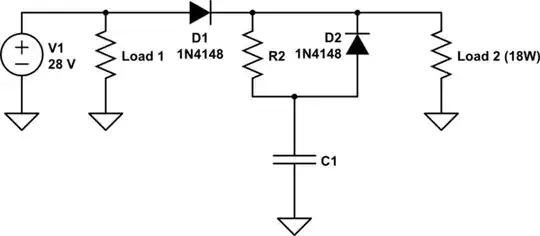
simulate this circuit
With this arrangament we can obtain a classic family of curves Vout = f(Vin) at four wiper's positions (K = 0.2 - 0.8).
STEP 6: Input voltage error visualized
But it is most interesting to investigate the voltage distribution along the pot's resistive film (aka voltage diagram). Thus we can see in another spatial way the "static error" (small voltage) at the op-amp input caused by the insufficient open-loop gain. I have shown below how we can do it with the help of CircuitLab and my recent invention - the "copy" potentiometer P2. If we connect it in parallel to the existing potentiometer P1, and move its wiper from one to the other end, we can measure the local voltages inside the potentiometer P1. We can then run a DC sweep simulation with parameter K.P2 and observe the voltage distribution.
In this conceptual circuit, I have used a generic op-amp, currently set to a very low open loop gain of 10x. With it, I have made an inverting amplifier with a gain of -1, "moving" the P1's wiper in the middle (its r2 = r1, K = 0.5). I have also moved the P2's wiper in the middle (its r2 = r1, K = 0.5).
simulate this circuit
As we can see, when "moving" the P2's wiper from left to right (changing the potentiometer's transfer ratio K from 0 to 1), the voltage drop linearly decreases from 1 V to -1 V. This is the voltage diagram of P2 that is a copy of the P1's voltage diagram. So what we see in P2 is the same as in P1. We can open the op-amp properties and start changing the gain from 1 to 300,000 or more while watching the op-amp input voltage. Then run the DC sweep simulation with parameter K.P2. As a result, you will see the voltage diagram below where the middle wiper's location (K = 0.5) is indicated by a thin vertical line in black and the zero voltage level - by a horizontal line in red.
As you can see, the local voltages along P1 (P2) linearly decrease from 1 V to -00 mV. Why do not they reach -1 V?
The reason is the very small op-amp gain factor (only 10). We can figuratively imagine the voltage diagram as a kind of Archimedean "lever" - the input voltage "raises" it on the left, and the op-amp output voltage "lowers" it from the right. But because the op-amp has very little gain, it does not have enough power to pull it up enough. There is an op-amp input voltage ("static error") of 98 mV at the midpoint of the potentiometer that is quite different from the zero voltage of a virtual ground, i.e. there is no virtual ground. In fact, there is a virtual ground, but it has "entered" inside to the right of the P1's wiper. Also, the circuit (inverting amplifier) gain is -0.8 instead -1.