Switched capacitor resistor

Question

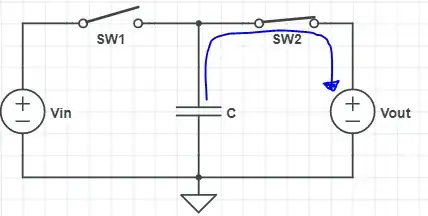
I have some basic doubts about switched capacitor resistors:

With this circuit we get an equivalent resistance equal to (Reference: Wikipedia):

Where f is the frequency of the clock signals that open and close S1 and S2.

My doubts are:

1. When we switch from S1 to S2 or vice versa, Cs has a certain charge and so a certain voltage, and at that instant a different voltage is applied on it. It is like short circuiting two voltage sources with different voltages. Where does the deltaQ (difference of charge) go, since there are no resistances?

2. Resistance means dissipated power. So if we get the behaviour of a resistor, there should be dissipation of power. But in this circuit S1 and S2 are ideal, and also Cs. Which is the explanation of this?

Answer 1

You are right, if we assume that the input is driven by an ideal voltage source and that we have ideal switches then the circuit can not be analyzed using our standard definitions of circuit elements. Connecting two voltage sources with different voltages in parallel results in an invalid circuit because it violates our definition of what "parallel" means.

At the instant after the switch closes the voltage on the capacitor must be exactly what it was at the instant before the switch closed. An instantaneous change in voltage across a capacitor would require an infinite current, which once again makes the circuit invalid and impossible to analyze.

Power is most certainly consumed in such a circuit, but it is consumed in the resistances of the real-world switches and real-world voltage sources rather than in the capacitors.

Answer 2

The problem of some papers and internet-contribution about SC-circuits is that the SC simulation of a resistor is not correctly explained. Please note that the shown simple circuit with two switches and one capacitor can take over the role of an ohmic resistor only if the most right node of S2 is connected (a) to ground or (b) to virtual ground or (c) to a capacitor much larger than the switched capacitor.

In any case, it must be possible that the switched capacitor is discharged when S2 is closed and, thus, ready to receive the next sampled voltage when S2 is open and S1 closed.

As an example, the wiki contribution shows how a SC integrator is realized. Here, the principle of the virtual ground is exploited and the charge is transferred to the capacitor in the feedback loop.

Answer 3

1. Consider the situation where Vin > Vout, and both are modeled by ideal voltage sources.

When S1 closes, the capacitor charges up to Vin and gets a charge of Qvin = C*Vin stored on its plates.

Now when S1 opens and S2 closes, initially the capacitor is charged to Vin, which is greater than Vout, but is also now connected to Vout. In general, an ideal voltage source will do whatever it can to make sure that it's producing its given voltage. In this case, the only way for that capacitor to lower its voltage to equal Vout is for enough charge to leave its plates, and the only path for this current is to sink through the ideal voltage source Vout. Vout will accept this current because it wants to establish its voltage on the connected node at all costs.

When this voltage is established, the charge on the capacitor is now Qout = C*Vout.

The value of the total charge transferred between Vin and Vout is then (Qvin - Qvout) = CVin - CVout = C * (Vin-Vout).

2. Since these components are ideal, the model of them will not have a power dissipation (real world will have parasitic impedances that will dissipate power). The reason it's considered a switched-cap "resistor" is because it behaves like a resistor in that a voltage difference across the circuit will have a deterministic and linear current output.