1

I desire to learn about "estimating the poles of a resonant signal", specifically the complex natural resonance of objects.

However, I don't know what "poles" are. What would you suggest I look up for better resources? :)

JRE
  • 67,678
  • 8
  • 104
  • 179
Sara Makboul
  • 45
  • 5
  • 1
    poles are where the system amplitude can head toward infinity, because of a denominator heading toward zero. Hence the amplitude is a POST or POLE sticking up out of the ground. – analogsystemsrf Oct 29 '19 at 10:24
  • 1
    [Intuition for resonant, natural, and oscillatory frequencies of RLC circuits?](https://electronics.stackexchange.com/questions/233654/intuition-for-resonant-natural-and-oscillatory-frequencies-of-rlc-circuits?rq=1) – Andy aka Oct 29 '19 at 11:05
  • 1
    [What are some insights from looking at Bode plots](https://electronics.stackexchange.com/questions/160140/what-are-some-insights-from-looking-at-bode-plots) – Andy aka Oct 29 '19 at 11:07
  • 1
    [What is the difference between frequency response and transfer function?](https://electronics.stackexchange.com/questions/275362/what-is-the-difference-between-frequency-response-and-transfer-function) – Andy aka Oct 29 '19 at 11:07
  • 1
    [Meaning of Sigma in Laplace transform](https://electronics.stackexchange.com/questions/316918/meaning-of-sigma-in-laplace-transform) – Andy aka Oct 29 '19 at 11:08
  • 2
    There is no such a thing as a "pole of a signal". It's not the signal that can have a pole but the **system**. – Curd Oct 29 '19 at 11:42
  • 1
    maybe the sequence of Youtube videos ["The Root Locus Method"](https://www.youtube.com/playlist?list=PLUMWjy5jgHK3-ca6GP6PL0AgcNGHqn33f) (by Brian Douglas) is helpful – Curd Oct 29 '19 at 11:50
  • 1
    Comment to the first comment: "System amplitude" should mean: The value (not the amplitude) of the complex transfer function expressed using the complex frequency variable s=sigma+j*omega. – LvW Oct 29 '19 at 14:00
  • 1
    The quotation marks indicate that you have read 'poles of a resonant signal' somewhere. Please give us that reference. Perhaps 'signal' should be 'system'. – Chu Oct 29 '19 at 22:45

1 Answers1

2

First of all, signals don't have "poles", systems do.

The transfer function of a system in many cases can be expressed as a ratio of two polynomials.

$$G(s) = \frac{A_ms^m + A_{m-1}s^{m-1} + ... + A_1s + A_0}{B_ns^n + B_{n-1}s^{n-1} + ... + B_1s + B_0}$$

There are values of \$s\$ for which the upper polynomial evaluates to zero. When that happens, the value of \$G(s)\$ must be zero, regardless of the value of the lower polynomial. These values of \$s\$ — the roots of that polynomial — are referred to as "zeros" of the transfer function.

Similarly, there are values of \$s\$ for which the lower polynomial evaluates to zero. When that happens, the value of \$G(s)\$ goes to infinity, regardless of the value of the upper polynomial. These values of \$s\$ — the roots of that polynomial — are referred to as "poles" of the transfer function.

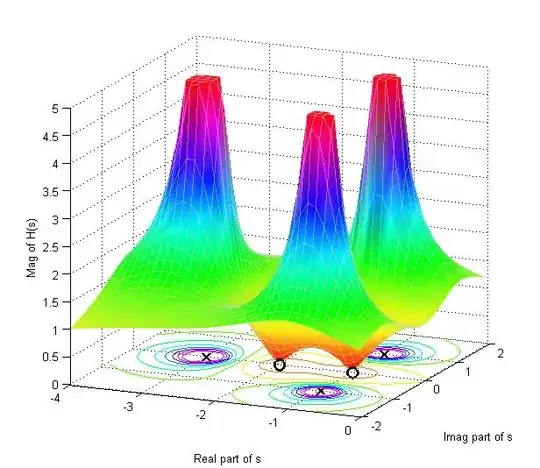
We sometimes imagine the response of the system — the values of \$G(s)\$ — as a "rubber sheet" that is stretched over the \$s\$ plane. The "zeros" of the transfer function are the places where that sheet is stuck to the \$s\$ plane, and the "poles" are frequencies where the sheet is pushed up by an infinitely tall pole, which is where the term comes from. In between, the sheet finds intermediate values that are determined mostly by the poles and zeros that are nearest to it.

Here's an example of such a visualization:

pole-zero plot

Source

Dave Tweed
  • 168,369
  • 17
  • 228
  • 393