3

The following circuit is supposed to output 1 if the input is greater or equal than 1010 (decimal 10). The truth table is given and we are supposed to convert that to POS and SOP using Karnaugh maps.
Here's the truth table with the minterms and the Maxterms:

Here's the Karnaugh map I did for the SOP (Sum of Products)

Sum of Products K-map

Same for POS (Product of Sums)

Product of Sums K-map

I remember my professor saying that when you make groups on the Karnaugh map if there's adjacent groups there will be a glitch.

I have three questions:

  1. Is it possible to fix the glitch without the Karnaugh map? If yes how?
  2. How do you fix the glitches on the Karnaugh map?
  3. How do you fix the glitches on the resulting circuits?
    (I have to make one for the POS and one for the SOP.)
greybeard
  • 1,469
  • 1
  • 4
  • 17
SilenceOnTheWire
  • 143
  • 5

3 Answers3

2

The term for this glitch effect is hazard. The Karnaugh map is an easy way to identify and eliminate hazards. A hazard exists when there are adjacent, non-overlapping groups (also called terms) in the K-map. When transitioning from one group to the other, the output shouldn't change according to the logic, but there might be a change or glitch because of uneven delays through the gates. If this is not tolerable, eliminate the hazard by defining an additional, redundant term that overlaps the groups, in effect bridging the gap between them.

For example, in your sum-of-products map, you have two terms, ab and ac. These two overlap; there is no hazard.

An example of a hazard: Consider the latch Q = DE + Q 'E (where 'E = not E). The latch function: when E is high, Q = D. When E goes low, Q maintains its level regardless of subsequent level of D. But there is a hazard: when D and E are high, Q is high and should remain high when E goes low. But both product terms change state, and if the DE term goes low before the Q'E term goes high, Q becomes 0. (The K-map will show that the terms do not overlap.)
To eliminate the hazard, add the additional, overlapping term DQ to the sum: Q = DE + Q'E + DQ

user28910
  • 3,849
  • 14
  • 18
0

No, you can never make sure there are no glitches in your design.

In real designs you find that glitches are caused by delays in the logic because one signal path is longer then another. You must make sure that glitches have gone by the time the signal get to the input of a register and the clock arrives. (Set-up time).

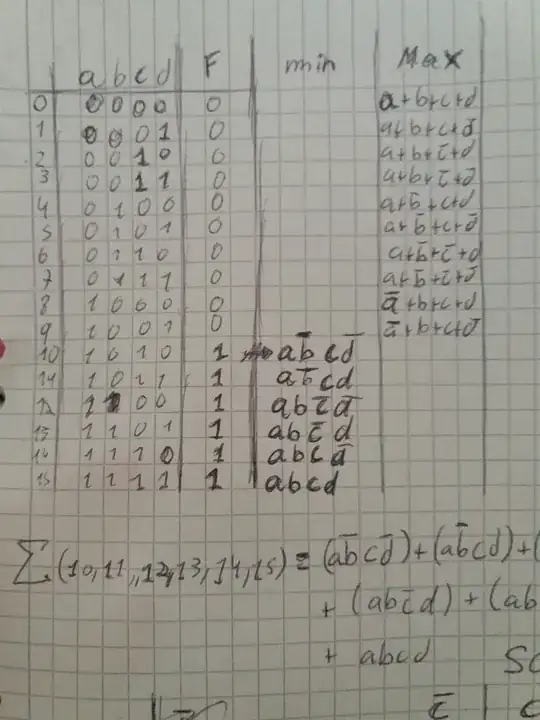
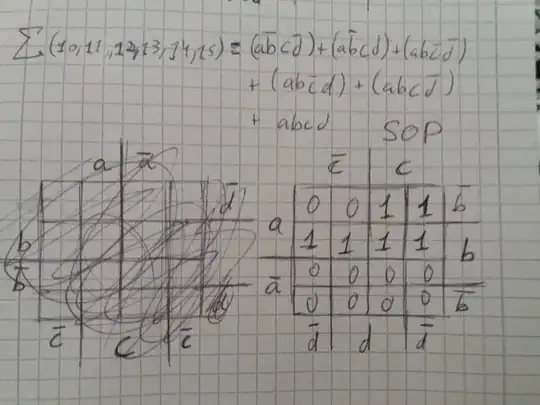
I had never heard of, lets call them "Karnaugh" glitches, and honestly to me they seem a typical 'academic' problem. To reduce a Karnaugh map you end up with AND, OR, gates and inverters. Each of these will have a different delay and then you have to add to that the delay of the output (The number of inputs to drive, plus the capacitance of the wires leading to them). Pass all that through a cloud of logic and you quickly realize that nobody can avoid glitches.

Karnaugh map are necessary for a fundamental understanding how logic works, However in in HDL design you do not make Karnaugh maps and use them to design an optimise circuits. Just this morning I answered a related question here where somebody did a lot of work to find the logic equations. You can see that the HDL solution ignores all that. What the actual logic is we leave to the synthesis tool.

I admit for the few people who design the synthesis tool, they had better know how to write programs to optimize logic. Also you might have to do some special work e.g. design a 6.4GHz serial I/O circuit. That is where the fundamentals of logic design come back and you have to calculate every gate. But 99.9% of the HDL designers know about Karnaugh maps, they can solve them (or they should be able to solve them...:-) , but they do not use them.

Oldfart
  • 14,212
  • 2
  • 15
  • 41
  • The problem is not about clocked or even extremly fast systems. For asynchronous combinational circuits it is enough if every input transition is covered by a gate. This is the Karnaugh method in the frame of this post (there is better name for it.). I agree that probably very few people do it. Maybe only a few analog guys who need some very minimal logic for their "programmable" circuit. Yes, I needed to do it once as well. – Horror Vacui Apr 10 '20 at 02:59
0

I can't quite reproduce it with this problem (I'm a bit foggy in the head from jet lag though)... But I definitely learned that you can remove glitches by making sure that every selected grouping in your karnaugh map overlaps another group, in such a way as to form a continuous chain. If this can't be done (for example with a simple xor) then you fundamentally have a circuit that will always glitch (like xor).

I have even used this at work, adding a redundant term to a mux that was implemented in and/or gates instead of a mux primitive (I'm an asic designer) to prevent glitches. The problem with the glitchy mux was that if select changes, even if both inputs are 1, the output can glitch 0. An extra term fixed it. Try it with a simple mux to see the difference.

Matt
  • 606
  • 1
  • 4
  • 6