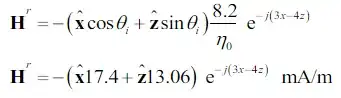Where do overtones in a 555 generated square wave come from?

Question

I have built a 555 oscillator and connected it to a speaker.

Using an oscilloscope I adjusted the 555 to generate a 2.5kHz square wave.

I then held a microphone up to the speaker and fed the input into a spectrum analyser.

What I expected to see was a single peak at 2.5kHz. However, what I actually got was this:

My question is, where have these harmonics come from if the 555 is only generating a 2.5kHz signal?

I know that a square can be constructed from sine waves:

However, the 555 does not generate sine waves or multiple frequencies, it generates a single square pulse. So where have these harmonic frequencies come from?

Odd harmonics are fundamental to a square wave as your second illustration shows. (It would be better explained as : a square wave can be decomposed into an infinite series of sine waves).. The even harmonics tell me the mark-space ratio is not 50%. — , Oct 20 '19 at 11:58
It's not that a square wave *can* be constructed from sine waves, as some optional thing or wacky view of it. A square **is** composed of sine waves. — TonyM, Oct 20 '19 at 12:02
@TonyM So then how can a 555 produce a square wave if this is the case? As far as I understand a 555 just switches its output on and off. It's not generating a bunch of harmonic sine waves and combining them. If a square wave can be generated by a 555 without having to combine sine harmonics then surely it is indeed optional? — JShorthouse, Oct 20 '19 at 12:07
The FFT (actually [a dft](https://en.m.wikipedia.org/wiki/Discrete_Fourier_transform)) is looking for sinusoidal content by definition. These are the glasses your spectrum analyzer is looking through. — relayman357, Oct 20 '19 at 12:09
With no disrespect, it sounds like your level of understanding doesn't yet extend to Fourier analysis of electrical waves. Don't be looking for a series of sine wave generators and a mixer circuit here. Your square wave is inherently just that. But you'll find plenty of explanatory text on this on the interweb. — TonyM, Oct 20 '19 at 12:29
@TonyM alright. I think part of this concept just clicked for me a minute ago, can you tell me if I'm on the right track? I'm sure there's a lot more to it than this but I've just realised that a square "wave" can't exist within the laws of physics because it would require voltages to instantly chance and electrons to teleport around. So this probably means that electrons can only move in sinusoidal patterns, and therefore any electrical signal has to be composed of a combination of these sinusoidal movements? — JShorthouse, Oct 20 '19 at 12:48
You're heading up a better mental road than you were but there's more to it. But as you know, this site isn't a tutorial but for seeding and encouraging self-learning :-) That's what you'll need to be a successful engineer and the volunteers here can't be expected to tutor. So, please be encouraged, forage on the internet and a little searching will find tons on this already written. — TonyM, Oct 20 '19 at 13:05
The square wave **is**. The 555 created it by switching the output. By feeding it into a spectrum analyser, you're asking the question 'what sine waves make up this square wave?'. If you'd fed it into a power meter, you'd be asking the question 'what's the power in this square wave?' BTW, the 555 generates an approximation to a mathematical square wave, because the output voltage can't switch infinitely fast. It's pretty fast compared to 2.5kHz, but not fast compared to 100MHz. — Neil_UK, Oct 20 '19 at 13:21
Re "What I expected to see was a single peak at 2.5kHz. ..." -> That would happen with a PURE 2.5 kHz sine wave and ideal test gear. Why would you expect all of a 2.5 kHz sine wave / square wave / triangle wave / sawtooth / infinite impulses / 1 uS wide pulses at 1V amplitude / ... - each at 2.5 kHz to produce a single 2.5 kHz peak? You have chosen a square wave as an arbitrary example of what SHOULD give a single peak. If you had chosen any of the others would you expect the same? Why? || NB - this is vital - You are not listening fully to what people are saying and are trying to cling ... — Russell McMahon, Oct 20 '19 at 23:38
... to your prior worldview. Learning tends to tear the brain (metaphorically) and you sometimes need to walk away from old visualisations (whicle noting the useful bits). A Fourier analysis is a tool for representing an arbitrary repetitive waveform by a set of sine waves. The results are "real" even if the means of arriving at the waveform seems unrelated. The infinitely sharp step is unachievable, but so is the infinite summing, the ability to see the infinite sums below the noise floor, the ability of the speaker to slew, ... . "All models are wrong. Some models are useful" :-). — Russell McMahon, Oct 20 '19 at 23:42
@TonyM "A square is composed of sine waves" - this holds for LC circuits, but it is not necessarily mathematically true. You can construct square-shaped functions in a dozens of ways, just think of the signum function which is a simple case distinction. — rexkogitans, Oct 21 '19 at 06:21
"Electrons can only move in sinusoidal patterns" This is not true. Voltages cannot instantly change and electrons don't jump around, but they move in whatever patterns they move. Signals are what they are. Sine waves (Fourier analysis) are a very useful mathematical tool to analyze motion and signals, but they're just a tool. The output of your circuit _consists of_ sine waves in exactly the same way a 5-inch-long stick _consists of_ five one-inch segments: you can choose to view it that way, but there are no one-inch segments in the stick itself. — Anton Tykhyy, Oct 21 '19 at 08:47
There are three parts to this: (i) roughly speaking you can represent any periodic signal as a sum of sine waves, (ii) spectrum analyzer shows what this decomposition looks like, and (iii) square wave of frequency f can be represented as the sum of sine waves at frequency n f each multiplied by 1 / n. This is why the spectrum analyzer shows those harmonics at higher frequencies. — copper.hat, Oct 21 '19 at 18:19
@Neil_UK Your comment is somehow better than any of the answers so far... — le3th4x0rbot, Oct 21 '19 at 21:41
There is no "can be" in mathematics; it is loose language that means the same thing as "is" when we examine it formaly. It's like saying, the number 6 can be made by adding 4 and 2. "But I just wrote down 6; I didn't start with any 4's or 2's in **my** 6; what are they doing in there?" — Kaz, Oct 21 '19 at 21:50
@trognanders maybe, but relayman said it first, I was just amplifying the point. — Neil_UK, Oct 22 '19 at 05:13
@TonyM I think it would be a lot more intuitive to say that it can be *analyzed* as a sum of sine waves, and that *is* an optional thing. It's not optional for square waves to have this property about how they can be analyzed as a sum of sine waves, but it is optional to actually do the analysis. — user253751, Oct 22 '19 at 08:59
@immibis As a silly nitpick, assuming QFT is true enough, ultimately every square wave _must_ be a combination of a ridiculous amount of sine waves. Even on a human-measureable level, a square wave is not really a square wave, since it takes a while to build up and drop down. Then you get into how you get power in the first place, which may be from an AC source converted to DC, which itself isn't a perfect, and even with a chemical battery, the response isn't perfect; you shouldn't really ever expect to see a perfect square wave. The question is, how much is too much? That depends on use. — Luaan, Oct 23 '19 at 07:41

score 36 · Answer 1 · edited Oct 22 '19 at 08:01

36

I know that a square can be constructed from sine waves. However, the 555 does not generate sine waves or multiple frequencies, it generates a single square pulse. So where have these harmonic frequencies come from?

Congratulations on your explanation of what you are seeing and your experimentation.

The key issue is that not only CAN a square wave be constructed from sine waves, it fundamentally IS a collection of sine waves.
You can generate a square wave by summing appropriate sine waves, but, however you do it, what you arrive at IS a waveform that can be represented by a collection of sine waves.

In ideal circumstances you would not expect to see on the spectrum analyser quite what you show, but impedance matching and a 555 and .... can easily combine to produce a non ideal result.

A square wave = a summation of \$ f + \frac{3f}{3} + \frac{5f}{5} + \frac{7f}{7} + ...\$ (if my brain has correctly retrieved the relevant long ago stored facts). So you would expect to see every second harmonic, and amplitudes should decrease.

edited Oct 22 '19 at 08:01

Melebius

109
5

answered Oct 20 '19 at 12:01

Russell McMahon

147,325
18
210
386

2

Is the answer here really then that a "square wave" isn't really a wave at all? I suppose that a true square wave can't exist within the laws of physics, it would require a speaker cone to teleport between two positions and electrons to teleport within a wire. Therefore because both electrons and speakers are constrained to moving in sinusoidal patterns, the only way to construct a square "wave" is by combining a bunch of sine waves together? – JShorthouse Oct 20 '19 at 12:31
6

@JShorthouse Electrons and speakers are not constrained to move in sinusoidal patterns. That constraint only arises for certain particular systems (e.g. harmonic oscillators). It so happens that sinusoids happen to be a convenient *basis* for analyzing systems that are linear and time-invariant, but you're reading too far into things. – nanofarad Oct 20 '19 at 20:38
@ζ-- Perhaps "constrained" is the wrong word, what I'm trying to say is that since a speaker cone has mass and momentum its movement is always going to be in a "curve-like" way, it's physically impossible for a speaker to replicate a mathematically perfect square wave. – JShorthouse Oct 20 '19 at 21:32
@JShorthouse Indeed, a model of a speaker may include a sort of "low-pass" characteristic. It doesn't change the answers here significantly. Sines simply remain useful eigenfunctions for analyzing linear time-invariant systems; a square wave is an infinite series of those sinusoids (a fundamental plus harmonics), and the "imperfection" of a square wave that makes it curve-like can often be described by the application of a suitable low-pass filter to the harmonics mentioned before. – nanofarad Oct 20 '19 at 21:34
3

@JShorthouse You can't have it both ways :-). You wrote "Using an oscilloscope I adjusted the 555 to generate a 2.5kHz square wave." You know you didn't, of course. A 555 makes a "squarish wave". Other devices more-squarish (or less). But just as the true square wave needs an infinite sum of declining magnitude sinewaves (and so extra terms are unimportant at somewhere around the noise level) so too viewing, analysing , ... is going to run into non-ideal or non-infinite aspects. A speaker is not constrained to follow a single sinusoid - but any path folows is describeable by a set of sinusoids – Russell McMahon Oct 20 '19 at 23:34
11

@JShorthouse It's not that square waves can't be fundamental, but the job of a spectrum analyzer is to analyze things in terms of sine waves, so that's what it did. When you analyze a wave in this way, of course you will see that only sine waves are "fundamental" according to this kind of analysis. – user253751 Oct 21 '19 at 15:23
1

@JShorthouse in large part you're right. An ideal square wave has infinite bandwidth and two discontinuities every period, and so can't be realized by any physical system. Only various approximations of it can. But that doesn't have an awful lot to do with why these answers are correct. – hobbs Oct 22 '19 at 01:13
3

at 2.5kHz, complaining the square wave can't be square is a bit like complaining your car's wheels can't be round because they're made of atoms. – user253751 Oct 22 '19 at 09:01

JRE · Answer 2 · 2019-10-20T12:41:12.333

A square wave can be viewed as a sum of the odd harmonics of a single frequency.

A square wave can be generated by summing a bunch of sine waves.

A square wave can also be generated by simply toggling the power on and off at the primary frequency of the square wave.

In either case, the spectrum will look the same.

You cannot tell how a square wave was generated by looking at the spectrum.

The simple act of turning the power on and off generates the primary frequency, but it also generates the harmonics.

Your spectrum shows even as well as odd harmonics.

The even harmonics are an artifact of distortion coming from your microphone or the microphone amplifier. Too much gain or the microphone too close to the speaker. Alternatively, the signal from the 555 caused distortion in the speaker.

In any case, you should only see odd harmonics (2.5kHz, 7.5kHz, 12.5kHz, etc.) for a 2.5kHz square wave. The even harmonics (5kHz, 10kHz, etc.) are not part of the square wave.

Connect the 555 output to the line in of your PC. You may need to use a voltage divider to reduce the level.

That should be cleaner, and closer to an undistorted square wave.

Baudline (the spectrum analyser you are using) has an oscilloscope view. Use it to check if your square wave is distorted. Check the signal from the speaker and microphone setup as well as the direct connection to the 555.

"Baudline (the spectrum analyse you are using) has an oscilloscope view. Use it to check if your square wave is distorted." thanks very much for this tip, the wave is indeed rather distorted. — JShorthouse, Oct 20 '19 at 12:25
"The even harmonics (5kHz, 10kHz, etc.) are not part of the square wave." - This assumes the mark/space ratio is exactly 50%. That's rarely the case in a typical 555 circuit. In this case it looks like the ratio was very asymmetrical. — Bruce Abbott, Oct 21 '19 at 03:33
@BruceAbbott: Absolutely correct. I was thinking only of nice, regular square waves with a 50% duty cycle. I should have mentioned that. I'd rather not change it just now, though. The question has landed on HNQ. If I go monkeying with it, it'll just attract more attention to a middling answer that's already gotten way more upvotes than is reasonable. — JRE, Oct 21 '19 at 09:25

Dave Tweed · Answer 3 · 2019-10-21T11:50:50.647

What I expected to see was a single peak at 2.5kHz.

I don't know why. You need to reset your expectations.

Think of this this way: If you just had a single peak, then the input would by definition be a sine wave. But you're feeding it a square wave, so how do you account for the difference?

I know that a square can be constructed from sine waves.

Change that to: A square wave is equivalent to an infinite series of sine waves. That's what the math of Fourier analysis is all about.

the 555 does not generate sine waves or multiple frequencies, it generates a single square pulse.

They are exactly equivalent. So it's actually doing both.

So where have these harmonic frequencies come from?

You can think of them as "coming from" the fast edges on the square waves. You can see in your own graphs that as you consider higher harmonics, the edges of the sum get steeper. In the limit (infinitely many harmonics), the edges become vertical.

copper.hat · Accepted Answer · 2019-10-21T22:51:21.990

16

When you are holding a hammer, the world looks like a nail.

Roughly speaking, a spectrum analyser captures a time record and represents the resulting capture as a unique linear combination of sinusoids.

It does not mean that whatever generated the signal generated separate sinusoids, only that the resulting signal can be represented in this (very useful) way.

As other answers have pointed out, a square wave can be represented by the sum of sinusoids at odd harmonics, hence the harmonics on your analyser.

There are other systems of representation (cf. Walsh functions) that represent signals in terms of square waves, however these representations are not practical from current perspective. However, if one had a mythical Walsh spectrum analyser and you looked at a sinusoid, your question might then be asking where do all the square waves come from.

edited Oct 21 '19 at 22:51

answered Oct 21 '19 at 22:38

copper.hat

837
7
16

2

"Yeah, yeah, but your scientists were so preoccupied with whether or not they could" ...read a square wave with a spectrum analyzer... "that they didn't stop to think if they should.". :) – longneck Oct 22 '19 at 15:13
5

They felt it was their duty to cycle through the possibilities... – copper.hat Oct 22 '19 at 19:45
1

Older spectrum analyzers did not capture a time record. They (HP 8553B, in HP 141 display) merely use selectable crystal-filters (for big buck, you get down to 10Hz resolution bandwidth). – analogsystemsrf Oct 23 '19 at 17:36
1

I know, I was born before the FFT was 'discovered' :-). Sweeping with a narrow tunable band pass is basically computing the Fourier coefficients directly. – copper.hat Oct 23 '19 at 17:54

score 3 · Answer 5 · answered Oct 20 '19 at 22:12

3

our ears are correlators. The FFT is a correlator. The analog spectrum analyzers of Hewlett Packard are correlators: they use narrow-band analog filters.

Square waves and rectangular waves, and many other (non-pure-sin) waveforms will strongly correlate with ( Positive_Integer * Fundamental) sin basis functions.

Square waves are not composed of sinusoids. The 555, and any FlipFlop, do not build the rail-rail outputs using a big bucket of handy sinusoids.

You ask a fine question.

We model, and we measure, using sinusoidal basis functions, harmonically related.

Examine the integral of sin(1,000 * time) multiplied by sin(3,000 * time). Do this for 1 cycle, for 1.5 cycles, for 1.6 cycles, for 1.9 cycles, for 2 cycles, for 200 cycles.

Harmonics do not exist. Its the behavior of the correlators that confuse us.

answered Oct 20 '19 at 22:12

analogsystemsrf

33,703
2
18
46

so the down-voters merely vote against this heresy, remaining unable to craft a lucid rebuttal? – analogsystemsrf Oct 21 '19 at 10:13
1

*"Harmonics do not exist."* Then how do you explain the difference between a sine wave and a square wave at the same frequency? How do you explain the operation of frequency multiplier circuits? If the harmonics do not exist, then how do we extract real power from them? – Dave Tweed Oct 21 '19 at 11:10
1

frequency multipliers first run the sin thru a distorter; the distortion then will correlate (be filterable) with the desired multiple of the fundamental. Next question, please. – analogsystemsrf Oct 21 '19 at 11:18
What is the waveform at the output of the distorter? Does it contain harmonics or not? You say they don't exist. – Dave Tweed Oct 21 '19 at 11:36
a pure sine of fundamental F will produce zero correlation, taken over a complete period of F, with any N * F pure sine, N being greater than 1. The distorter output can be described with polynomials, series approximations, with scale factors such as 1/1, 1/3, 1/5, 1/7, 1/9 ... and correlations at exactly those Nth factors higher than the fundamental will indeed produce the computed amplitudes predicted by the distorter polynomials. And a spectrum-analyzer also produces the amplitudes. Yet the distorter has no bucket of integer-frequency N * F scaled sines and cosines for composing Vout. – analogsystemsrf Oct 21 '19 at 17:27
Its just the math. Fourier was very skilled. He wanted to solve differential equations, to fit arbitrary heat-equation shapes and predict solutions. His method uses Fundamental sins and N * F sines to compose those solutions. A FlipFlop has no bucket of F and N * F sins to use. – analogsystemsrf Oct 21 '19 at 17:31
key insight-- a very fast edge will trigger ringing (indicating some correlation) with **ANY** resonator. We can watch the ringing decay, because there was only ONE edge. Now --- increase the repetition rate, and watch the ringing amplitude be a strong function of the relation between resonator **bandwidth** and the fast-edge repetition rate. I've done this, when fresh out of university, and had to realize the stored energy in the resonator ---- memory of edge timings --- was rising and falling as the frequency changed. Yet only energy into system was ---- a fast edge that triggered ringing. – analogsystemsrf Oct 21 '19 at 17:39
1

This answer makes the most sense to me, I don't know why it's being downvoted so heavily, can anyone give a proper rebuttal? From quickly searching around it seems widely accepted that the human ear performs the equivalent of a Fourier transform (which has blown my mind somewhat). But this would clearly explain why you can hear harmonics in a signal that was generated by merely switching an output from rail to rail, and why a spectrum analyser sees the same thing. Like another commenter said, a 5cm stick can be said to be made of five 1cm segments, but that doesn't mean it was made that way. – JShorthouse Oct 21 '19 at 18:12
1

@JShorthouse our ears don't perform the equivalent of a Fourier transform, they do something much more simple and basic. Responding to sine waves is something that many (in some sense, almost all) physical systems do. Harmonics do exist, not just as a figment of the math, but as part of the behavior of real things. Digital circuits are an idealization; all *real* circuits are analog. The circuit is full of electrons that are very willing to do sine-wavey things, and its imperfections are well described by how it responds to some of those higher-frequency sines. – hobbs Oct 22 '19 at 02:28

score 2 · Answer 6 · answered Oct 20 '19 at 12:31

2

I would suggest that it's due to semantics, and those semantics falsely colour our perspective of a square wave. The following is the internal architecture within a 555 chip:-

You can clearly see that it's a digital circuit (rise/fall times excepted). It does not output a series of sine waves, exactly as you suspect. The output toggles between high and low voltage levels. So you're correct.

But mathematically (and taking from Wikipedia), a theoretical square wave can be represented as an infinite summation of odd sine harmonics, thus:-

You can see the \$sin\$ operator in there. It's just that your spectrum analyser can't tell the difference. After all, you might be feeding it an analogue summation of a few sine wave oscillators all running at odd harmonic frequencies. It would be indistinguishable from a square wave.

Also don't forget the speaker, microphone and recording equipment, which are inherently analogue and have physical mass i.e. smoothing. Some peaks will therefore come from a unintentional filtering effects of your audio equipment.

answered Oct 20 '19 at 12:31

Paul Uszak

7,327
5
37
69

1

A digital circuit is merely 'convenient analogue'. It's a circuit composed of analogue components that uses a simplified mode of operation. It's inputs and outputs still have analogue characteristics, as this question is showing. Meanwhile, a square wave being composed of sine waves isn't semantics, it's physics. – TonyM Oct 20 '19 at 13:15
3

@TonyM Hmm, I'm not sure. I think the interpretation is on behalf of the spectrum analyser. Otherwise, how is the inverter on pin 3 producing a 7.5 kHz sine wave? Where is that 7.5 kHz oscillator circuit? That's what you're suggesting it's doing. It's the same kind of mathematical trick/FFT/interpretation that _proves_ that you can never reach where you're going by iteratively halving the remaining distance. – Paul Uszak Oct 20 '19 at 13:54
If you split white light, you realise it's composed by a 'mixture' of a spectrum of colours. That doesn't mean there's two 'white light's in existence: the one you see when you split it, the one you knew when you didn't. It means what you thought was an element is actually a compound, roughly speaking. Ivm afraid it reads like you should be reading the other answers, not writing one, downvoting accordingly. – TonyM Oct 20 '19 at 14:33
1

@TonyM Your's is a great example of what I mean. We're not making the white light in the first place are we? For light read square wave. There is no 7.5 kHz oscillator circuit to make the first harmonic in the 555, is there? Plus you'll find that this answer is entirely consistent with the others. Semantics :-) – Paul Uszak Oct 20 '19 at 17:06
I think you've missed the point by a mile and I imagine you think the same about me so we're going nowhere. I'll leave you in peace and wish you well :-) Pleasure talking, if you want to continue in chat I'd be happy to there. – TonyM Oct 20 '19 at 17:12
1

@TonyM Does that mean a sine wave is fundamentally composed of Walsh functions? (like another commentator said) – user253751 Oct 22 '19 at 09:08

Where do overtones in a 555 generated square wave come from?

6 Answers6

Linked