I need some explanations about Linearity, Negative Feedback and Virtual Short for an ideal Operational Amplifier.
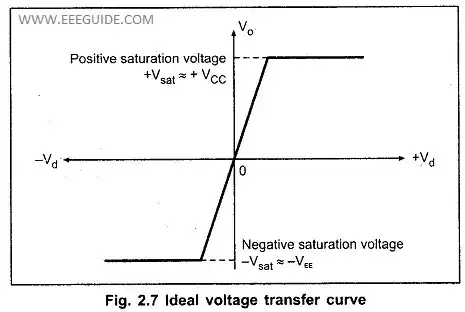
Precisely, I have been always told that an operational amplifier with negative feedback works in linear region, i.e. that with the diagonal straight line in the following picture:
Now I always saw this reasoning: since the negative feedback forces the op-Amp in the linear region we may write that A = Vout/(V+-V-). Now, since A is very high, ideally infinite, we get that (V+ - V-) = Vout/A = 0. This property is called virtual short between op-Amp input terminals.
My question does not regards this last step (which I saw also in many topics here) but the sentence "the negative feedback forces the op-Amp in the linear region": why? Why does the connection of the output terminal to the inverting input terminal determine this condition? I think that probably I should know the internal structure of an op-Amp to understand it correctly, but can you give me a brief explanation?