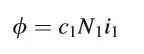As always with finite element analyses, specific expressions for certain quantities can only be given if the basis functions psi(x) are known. I don't know if there is a standard system of basis functions for Voronoi meshes, but in general the potential function of your system will be linearly parameterized somehow by the nodal values of the electric potential.
$$\Phi(x)=\Phi(\phi_1,\dots,\phi_n,x)=\sum_k\phi_k\psi_k(x)$$
The specific values of the nodal potentials will be calculated by solving Gauss' Law within the FEA framework under the given boundary conditions. This reduces to a linear system of equations, which I suppose you have already solved by your software.
On the other hand the continuum form of Ohm's law generally states for current density
$$j=\sigma E=-\sigma \nabla \Phi$$
or for our finite element case
$$j(x)=-\sigma(x) \nabla_x \Phi(\phi_1,\dots,\phi_n,x)$$
If you want to know the current through a facet A_ij of a Voronoi cell V_i, you have to integrate current density over the surface area of the facet. For your planar problem this is effectively going to be a line (with normal n) integral and a multiplication with the layer height.
$$I_{ij}=\int_{A_{ij}} (j\cdot n)dA=h\cdot\int_{s_{ij}} (j\cdot n)ds$$
Due to the specific Ansatz for the electric potential this is going to yield
$$I_{ij}=-\sum_k\phi_k\int_{A_{ij}} \sigma(x)\nabla\psi_k(x)dA=\sum_k\phi_k\Gamma_{kij}$$
where Gamma is the conductance matrix of the discretized system. The crucial point here is that there is no way around relating the conductance matrix to the chosen basis functions. In other words, the basis functions determine what it means that the electric potential has certain values at certain nodal points. Without specifying the basis functions, the potential between the nodes (and hence at the current integration surface) could be anything that satisfies Gauss' law, and that is a pretty lot of freedom.
If the basis functions are designed in such a way that the behavior of the potential on the interface A_ij only depends symmetrically on the nodal values phi_i and phi_j, the conductance matrix will be of the form
$$\Gamma_{kij} = G_{ij}(\delta_{ki}-\delta_{kj})$$
So only in this special case the "conductance between cell i and cell j" is defined and current takes on the form
$$I_{ij}=G_{ij}\cdot(\phi_i-\phi_j)$$
Likewise you can compute the resistance as the reciprocal of conductance
$$R_{ij}=1/G_{ij}$$
The "nuisance" that an FEA quantity (like Gamma above) might, in the general case, depend on more than the "naive" number of nodes is also known from other application fields. For example in structural mechanics we might encounter a "mass matrix" where masses are neither point masses nor extended rigid bodies, but rather some entities that act on multiple nodal coordinates. That is generally a certain obstacle when it comes to naive physical interpretation. In your case this could apply to the ability to interpret the system as a "resistor network", depending on how nasty the specifically chosen basis functions are.