Unity Gain Buffer Initial Conditions

Question

schematic

^{simulate this circuit – Schematic created using CircuitLab}

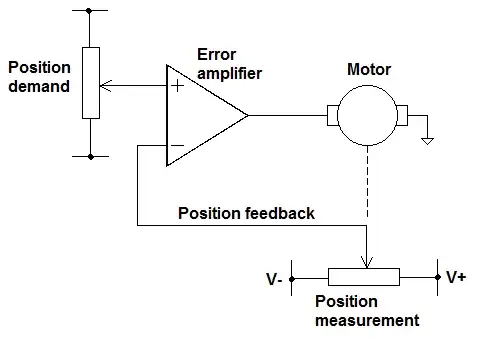
A typical way of analysing the unity gain buffer is:

Where A is Open Loop Gain

Vout = A(Vin - Vp) and Vp = Vout therefore

Vout = A(Vin - Vout)

Vout = AVin - AVout

Vout + AVout = AVin

Vout (1+A) = AVin

Vout / Vin = A / (1+A)

if A >> then 1+A ~ A

Vout / Vin = A/A = 1

I would like to get an understanding of how this works from initial conditions ie step response

At t= -1 Vin, Vp and Vout = 0

At t= 0 Vin = 1V and as Vp = 0, Vout = A(1-0) = A

As Vout = A then Vp = A such that Vout = A(1 - A) = A - A^2

Subbing again gives Vout = A(1 - (A-A^2) = A(1-A+A^2)

This is obviously just going to run away so must be incorrect, perhaps it is my initial condition assumption that is wrong?

Alternatively using the simplified model of an op amp:

I could assume that at t=0 Vp = Vin therefore Vout = Vin

However Vin = A(Vin - Vin) is a contradiction

Obviously this is a well known circuit so I must have a fundamental misunderstanding but what have I got wrong?

*Edit

Just to clarify the purpose in asking,

I'm trying to get an understanding of how negative feedback works. The standard analysis at the start of the question is effectively time independent and I would like to know how the output rises with time

Well at t = 0 Vp and Vout do not equal Vin (unless you're assuming Vin hasn't received the electric field yet produced by the source which gives Vin its voltage value. Nothing happens instantaneously in physics... Initially the gain is *not* unity otherwise the Vout would never rise from 0V to matching Vin. Of course, this period of rising is very, very quick. You can't take the ideal op amp rules to the extreme. They are general guidelines for solving for steady state conditions as well as accurate estimates. — Andrew, Aug 23 '19 at 11:30
Thanks, I get the point that the rules I'm trying to apply are only approximations but what mathematical analysis should I use to determine how negative feedback works to achieve unity gain? I suppose the simplified rules look at an opamp as a black box that acts as a mathematical function — andowt, Aug 23 '19 at 11:40
Yes, to an extent. Remember Vcc and Vee supply the op amp with the ability to provide that negative or positive feedback (cc standing for common collector and ee for common emitter) so it's not entirely some magical process by which the op amp produces voltage gain - it does so drawing from its own supplies (which means it cannot output more voltage than its negative or positive supply). But yes, op amps have internal workings involving transistors i'm not familiar with. Sorry mate — Andrew, Aug 23 '19 at 12:14

score 1 · Answer 1 · answered Aug 23 '19 at 11:51

1

I'm trying to get an understanding of how negative feedback works.

Think of it like a control system and an error amplifier.

You set the "demand" on the non-inverting input and the negative feedback causes the op-amp output to rapidly change to a voltage that makes the input error minimal. In other words, the inverting input is made to be nearly the same voltage as the "demand".

Because the open loop gain is massive at low frequencies, the amount of error required to "drive" the control system into stabilization is quite small.

You can, if you want, regard the op-amp as a kind of motorized control system: -

When you grasp this, replace the motor and position measurement potentiometer with a wire link and you have a simple op-amp buffer. It's easy after that!

Picture from this q and a.

answered Aug 23 '19 at 11:51

Andy aka

434,556
28
351
777

This has been my working knowledge of op amps so far and enabled me to design with them however i'm trying to understand how the op amp actually does this. This is the closest Ive found so far https://www.physicsforums.com/threads/how-does-negative-feedback-in-an-op-amp-work-conceptually.584881/ Effectively saying that when the input is applied the output has a finite rise time but it dosent explain why the output would stop rising – andowt Aug 23 '19 at 12:25
The output stops rising when the input equality is reached plus or minus a small error. Once the inputs are within the error margin of being the same, there is nothing to amplify hence the output stops changing. – Andy aka Aug 23 '19 at 14:34
Any reason for the downvote? – Andy aka Aug 26 '19 at 08:39
Not entirely sure who or why, not the answer I was looking for but still adds to solving the question imo so +1 from me! – andowt Aug 27 '19 at 08:45
Maybe say what you are more specifically looking for? – Andy aka Aug 27 '19 at 17:44
My question provided both an illustrative example of the type of mathematical analysis I was looking for as well as mentioning that I wanted to gain an understanding from initial conditions. The edit mentioned that I was specifically interested in how the output rises and stabilises with time. Your answer only addressed one sentance out of the entire question which Is why i assume someone down voted you. I upvoted as I thought your answer added a different way of thinking but didnt answer the question. Im open to suggestions of how I could have asked the question more specifically? – andowt Aug 28 '19 at 09:15

Justin · Accepted Answer · 2019-08-23T14:31:51.150

When you are considering a step response, you need to include the time delays at the different locations for the answer to be reasonable. One way to model this is to add an RC filter at the output of the op-amp. The other thing that you haven't accounted for is that the op-amp can't actually drive the output to greater than the positive supply voltage.

Taken in combination, and assuming Vs = 5V, this means after the positive input steps from 0 to 1, the output of the op-amp would follow a curve something like this, ignoring feedback for now:

OK, now what happens if we do include feedback? Remember that the negative input to the op-amp is the same node as the op-amp output. Once the output starts to get close to 1 V, the op-amp will begin to drive less current. In particular, once \$V_{out} > 1\text{ V} - \frac{5\text{ V}}{A}\$, the output stops driving high as hard as possible. This doesn't mean it flattens out immediately, but the endpoint/goal of the RC settling starts to drop. I will call this goal point Vfinal and I've plotted it alongside Vout in the plot below:

Zooming in to the time when Vfinal drops:

Here is the schematic for the above plots (though I actually just simulated them in python):

schematic

^{simulate this circuit – Schematic created using CircuitLab}

Python to generate the above plots, if you are interested:

from matplotlib import pyplot as plt
import numpy as np
a = 1000
vp = 1.
vs = 5.
ts = np.linspace(0, 0.3, 10000)
v_rc = 5.0 * (1.0 - np.exp(-ts))
# plt.plot(ts, v_rc)
# plt.axis([0, 8, 0, 5])
# plt.xlabel('time (# time constants)')
# plt.ylabel('voltage')
# plt.show()

vout = 0.
vfinals = [0.]
vouts = [0.]
for i, t in enumerate(ts[1:], 1):
    vfinal = a * (vp - vout)
    vfinal = np.clip(vfinal, 0., 5.)
    vfinals.append(vfinal)
    dt = t - ts[i - 1]
    dv = (vfinal - vout) * dt
    vout += dv
    vouts.append(vout)

plt.plot(ts, vouts, '-', ts, vfinals, '--')
# plt.axis([0.21, 0.24, 0, 5.1])
plt.axis([0.22, 0.233, 0.98, 1.02])
plt.xlabel('time (# time constants)')
plt.ylabel('voltage')
plt.legend(['Vout', 'Vfinal'])
plt.show()

This has helped clearly explain whats going on relative to time. It would be useful to have an even more zoomed in graph to show that once settled Vout != V+ as this was a sticking point for me. I've accepted this as the answer as its done the most to get my head around it but ill also add another answer to show the conclusion I've come to — andowt, Aug 27 '19 at 08:15

score 0 · Answer 3 · answered Aug 27 '19 at 08:43

In addition to Justin's answer here's a mathematical way of looking at it:

Using Vout = A(Vp - Vn)

The incorrect assumption that I was making was that Vout == Vp == Vn which is wrong as: Vp - Vn = 0, which is a contradiction as this would make Vout = 0

Looking as Justin's answer we can see that Vout (and therefore Vn) start at 0v and rises with time until it flattens at a value near Vp (Which we now know cant be Vp)

So as a conjecture, is it possible that for some small value d and a given value of Vp that Vout and Vn both equal (Vp - d):

(Vp - d) = A(Vp - (Vp - d)) = A(Vp - Vp + d) = Ad,

Giving:

Vp = Ad +d = d(A+1)

Therefore:

d = Vp / A+1

Testing this with values: Vp = 1V, A = 1000

d = 1 / 1001 ~ 9.99E-4

1 - 9.99E-4 = 1000(1 - (1 - 9.99E-4))

1 - 9.99E-4 = 1000(9.99E-4)

0.999 = 0.999 - conjecture proven

Adding to this, in the case of increasing or decreasing Vp (in unsaturated operation)

if Vp increases then the output will rise as Vp - Vn has increased until Vout (and therefore Vn) reaches (Vp - d)

if Vp decreases then Vp - Vn will have decreased meaning Vout will decrease in turn reducing Vn until Vn = (Vp-d)

Hopefully this explanation helps others as the combination of this and Justin's' answer makes it far easier form me to understand how negative feedback works as opposed to what it does.

Unity Gain Buffer Initial Conditions

3 Answers3

Linked