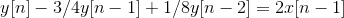Interpretation of the pole of a transfer function of a vibrating platform

Question

I am not able to understand what the frequency where the hydraulic pole occurs (as in the diagram) signifies? To give an overview, there is a vibrating platform and we are seeing its response motion at different input frequencies using an inductive position sensor (IPS). Now I know poles are points where the transfer function’s denominator is zero. But what does that translate into for a real life system? I was guessing that it might be the point where the amplitude of motion becomes maximum (in reality it can’t become infinity hence this thought). But in the diagram, I just can’t figure out what makes the pole point’s frequency (around 20 mHz) special? My reasoning might be awful and I apologise if that is so.

Answer 1

As @jDAQ said, poles are the roots of the characteristic equation.

But a pole can take a real value or come as a complex pair, and your response plot is for a sine wave sweep -- and in the Laplace (s) domain the only frequencies in a sine wave are \$\pm j \omega\$.

A good physical interpretation of a transfer function such as \$H(s) = k/(s + a)\$ is that the system will have a strong response to sine waves at frequencies below \$\omega = a\$, medium at \$\omega = a\$ (strictly speaking, at half power), and diminishing response above. Another one is that the system has a time-domain response containing the exponential \$e^{-at}\$. Both of these are consistent with one another -- they're just two different ways of looking at the same problem.

Answer 2

Poles are the roots of the characteristic equation (the denominator of the transfer function), so if you have a transfer function such as: $$ G(s) = \frac{1}{s^2+a \cdot s+b} $$

That can also be rearranged to look like this, $$ G(s) = \frac{1}{(s-s_1)(s-s_2)} $$

where \$s_1,s_2\$ are the poles of it.

You are correct that,

Now I know poles are points where the transfer function’s denominator is zero.

But, when you are inputing a sine/cosine to the system you should look at the response for the Fourier transform $$ G(j\omega) = \frac{1}{(j\omega-s_1)(j\omega-s_2)} $$ where \$\omega = 2\pi \cdot f\$. Notice that, any of the poles can have the form \$ s_1 = x+ jy\$. So, a term of the form \$(j\omega-s_1)\$ will be able to "zero" the imaginary part of the pole, but not the real part, that will remain unchanged. That is why inputing the right frequency can result in a peak output but not a infinite one. Observe this, if the system can be represented as

$$ G(j\omega) = \frac{1}{(j\omega+a+j)(j\omega+a-j)} $$

and for, $$ G(j) = \frac{1}{(a+j2)(a)} $$.

For a very small \$a\$, let say,

$$ a=0.001 -> G(j) \approx \frac{1}{(j2)(0.001)} = \frac{1000}{j2} $$.

These are cases where you have a peak, when the pole is very close to the imaginary axis. Then, by inputing the right frequency the output will have a big gain. But, if \$a\$ is large, such as

$$ a=100 -> G(j) = \frac{1}{(100+2j)(100)} \approx \frac{1}{10000} $$

there is no peak. At peak at a pole is discussed the same confusion on poles leading to a very big output. The resonant frequency happens when you have a pole on the the imaginary axis or very close to it, then the system tends to oscillate increasingly.

At slide 14 you can see a nice graph on the different behaviors that can be observed at the pole frequency, also, note that it is also explained the approximations usually used on bode plots. In these approximations, it is said that after a pole (as the frequency increases) the amplitude of the signal decreases 20dB/decade, while after a zero it increases 20dB/decade. But that is just an approximation! After all, the two examples I gave show the amplitude of the output for a signal with the frequency of the pole can either cause a peak or not.