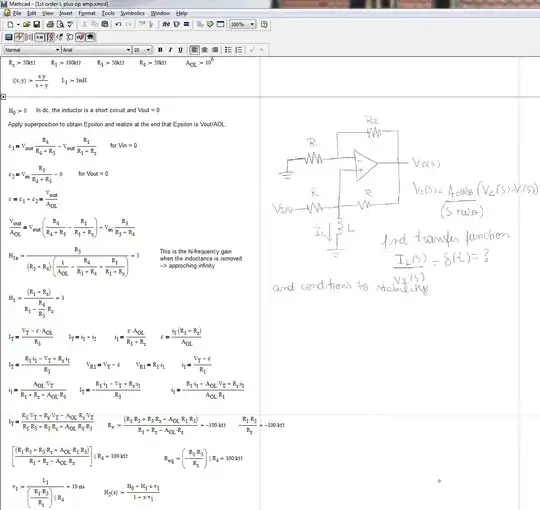
Mutual capacitance sensor behaviour

Question

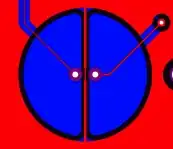
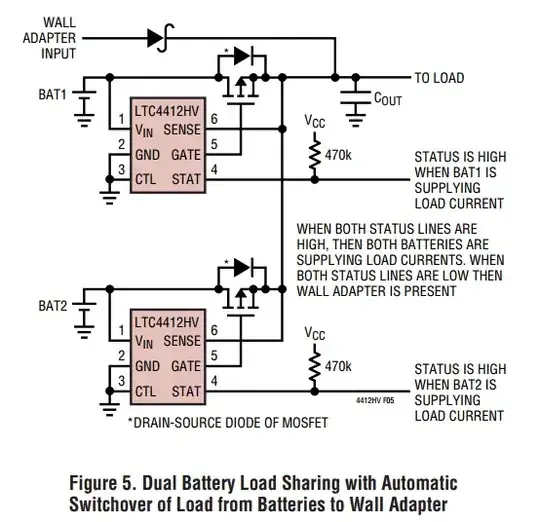
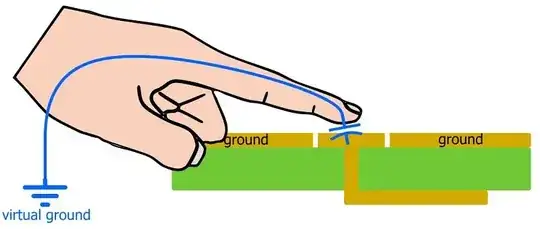
In a typical mutual capacitance touch sensor when finger approaches sensor it draws electrical field in effect decreasing the capacitance of the sensor (which is described here and here, for example).

Now, I came across this sensor design and tried to work out the principle of how it's working.

Here, the receive signal (left) is separated with transmit signal (right) via ground (and is also surrounded by it) and instead of a finger, there is a conductor (insulated from GND using a rubber cup) moving in or out above the sensor.

My understanding is, that this sensor is (with respect to the above "usual" situation) normally closed (i.e. electric field lines flow to the GND strip in-between Rx and Tx pads) and when the object approaches these pads it diverts them and increases the mutual capacitance of the sensor.

Is this reasoning correct?

"normally closed" is a very loaded phrase. A switch is closed when its resistance is low, and open when the resistance is high. Capacitive impedance is low when the capacitance is high, and high when the capacitance is low -- so your phrase reads "backwards". — TimWescott, Jul 02 '19 at 14:50
Do you have a reference for your first example? Give us a link? Whether the approaching finger increases or decreases capacitance to ground depends on the geometry of the board; I'm not sure even as drawn that the finger there isn't actually *increasing* the capacitance from the active pad to ground. — TimWescott, Jul 02 '19 at 14:52
@TimWescott I added links to the question. As for "normally closed" I was speaking roughly in terms of digital logic, where "closed" would mean "touch detected" and "open" otherwise. — mewa, Jul 02 '19 at 15:03
Thanks. I think the DigiKey drawing is more clear, but that's just an opinion. — TimWescott, Jul 02 '19 at 15:13
@mewa How detailed of an answer do you want? The basics of this is what happens to the dielectric dipoles in the dielectric and how the finger interacts to effectively increase the dielectric path length over part of the electric field curvature. The statement is correct in that the capacitance decreases. But the details are both simple (on one hand) and semi-complex (on another.) How difficult the detailed discussion is depends on just how much detail you need and how familiar you are already with round trip path integrals of the electric field. — jonk, Jul 06 '19 at 06:04
@jonk Thanks for replying! I'm mostly interested in a high level overview. What would be of much use is a description of the behaviour taking into account the fact that the object coming in proximity is a conductor that is insulated from ground. I wouldn't mind a couple links or equations so I can go deeper and learn something as a follow-up but the high level view is what I'm mostly after. — mewa, Jul 07 '19 at 21:01
@mewa I would probably recommend that you read Chapter 17 of the 3rd edition of "Matter & Interactions" by Chabay and Sherwood. Pay particular attention to the pages around 691, or so, where they discuss the round-trip potential, dielectric dipoles, and the definition of the dielectric constant. Their discussions leading up to that point are what make it easy to see what you are asking. If you sketched out the dipole alignments in the electric fields related to your question (and understood why) then I think the rest isn't hard to see. — jonk, Jul 07 '19 at 21:07
@jonk Thanks, I'll have a read when I have a moment. I could use a refreshment, it's been so long since I've had proper exposure to physics... — mewa, Jul 09 '19 at 22:02
@mewa I considered the idea of trying to write it out and decided that if I wrote only a little, it honestly wouldn't be enough and would beg more questions. I could attempt this in a week or so. In the meantime, just keep in mind we are talking about the finger changing the geometry of a system of mutual capacitance with overlapping receiving and transmitting "plates." The effect is to pull away charge. But the system model is complex. See perhaps starting on page 21 of this [Touch Tutorial](http://www.walkermobile.com/Touch_Technologies_Tutorial_Latest_Version.pdf)? — jonk, Jul 09 '19 at 22:28
@jonk Thanks! I did stumble upon this chart on page 22 and I think it more or less explains how it should behave. In my case, there is no finger only a conductor plate, insulated, which rules out ground connection and essentially means the circuit behaves like laptop2d explained below. — mewa, Jul 12 '19 at 13:43
@VoltageSpike Yes, thank you. Could the GND strip still be ignored if it was a finger approaching the sensor instead? — mewa, Jul 22 '19 at 21:46
The problem with only a finger is a finger would be modeled as a capacitor, but the other end of the capacitor is connected to everything else in the room because the field lines Fingers have a different conductivity, so that would need to be accounted for also. It's easy to model a conductor, but harder to model something that's in between. — Voltage Spike, Jul 23 '19 at 17:13

Voltage Spike · Accepted Answer · 2019-07-10T16:55:25.540

Your reasoning is correct, the capacitance increases if the conductor gets closer to the PCB. The system could be modeled as two capacitors in series, the fringing effects of current/field lines above the conductive plate could most likely be ignored (depends on how close other objects like a finger get to the top conductive plate, or if there is an insulative separator above the plate). Fringing fields to ground would probably also be minimal if the plate is close to the PCB.

Anyway lets say the conductive plates have an area of 1cm^2 and the distance is 1cm (for easy maths sakes. I'll also neglect the electric permeability for this demonstration)

\$ C= \epsilon\frac{A}{d}= \frac{1}{1} = 1\$

Then lets say we depress the conductive plate, and change the unit distance between the PCB to 0.5 (so the plate is closer).

\$ C= \epsilon\frac{A}{d}= \frac{1}{0.5} = 2\$

So when the plate is closer, the capacitance is larger.

The change in the gap material could also affect the capacitance (by changing the electrical permeability as there would be less air in the gap). But the effects of the material would most likely be small when compared with the change in distance.

You could get some rough cut numbers of capacitance by finding the surface area of the conductors and the distance between the plate and the PCB.

score 0 · Answer 2 · answered Jul 08 '19 at 05:51

Human flesh is a good dielectric material, because our body is largely made up of water. The dielectric constant of a vacuum is defined as 1, and the dielectric constant of air is only slightly higher. However, the dielectric constant of water is much higher, around 80. The interaction of the finger with the electric field of the capacitor thus increases the dielectric constant and thus the capacitance.

Therefore, the finger can be seen as the second conductive plate of an additional capacitor (And we know, two capacitors in parallel will increase the overall capacitance).

My understanding is, that this sensor is (with respect to the above "usual" situation) normally closed (i.e. electric field lines flow to the GND strip in-between Rx and Tx pads)

No, capacitive changes are detected by changing the charge and discharge times. This means that the increased capacity (caused by the finger) causes a longer charging and discharging time of the total capacity.

For more details please look here:

https://www.allaboutcircuits.com/technical-articles/introduction-to-capacitive-touch-sensing/ https://www.allaboutcircuits.com/technical-articles/circuits-and-techniques-for-implementing-capacitive-touch-sensing/

Thank you for your answer, but what you described is a self-capacitance sensor, whereas I'm inquiring about a sensor operating on the principle of mutual-capacitance (i.e. transmit and receive lines are capacitively coupled together). — mewa, Jul 08 '19 at 21:57

Mutual capacitance sensor behaviour

2 Answers2