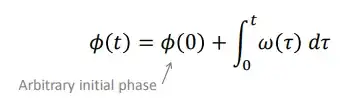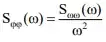I have a doubt on the relationship between phase and frequency. We know that the definition of angular frequency is:
ω(t) = d(\$phi\$(t) / dt, where \$phi\$(t) is the istantaneous phase of our signal.
In this case ω(t) is a function of t. We can write:
If we pass to Laplace domain, we get:
Is it correct to say that, if we want to pass to Fourier Transform, s = jω, and so writing
\$phi\$(jω) = ω (jω) / jω
?
It seems quite strange to me (I think that s = jω represents the angular frequency of the signal "angular frequency" ω(t), and so not equal to jω), but somewhere I read this statement.
For instance, I saw this statement for proving that the Spectrum (power spectral density) of Phase noise is bounded to that of Angular frequency through the relationship: