3

I have a full bridge SMPS and I am measuring the voltage across the output´s diodes on the secondary side.

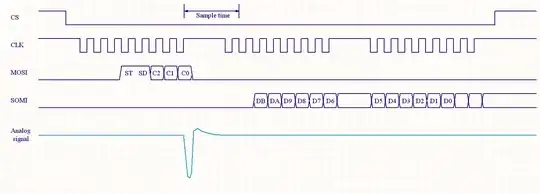
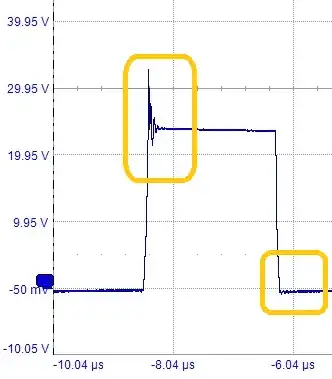
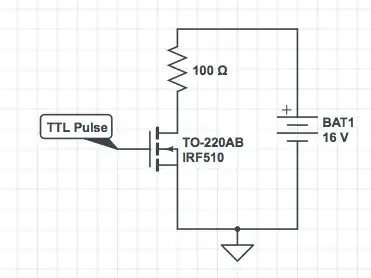
enter image description here

As you can see the voltage spike changes by changing the output current, for example at zero output current the spike is arount 32V,

enter image description here

while at 14A it is around 41V.

enter image description here

It means the poles of the transfer function of full bridge SMPS are moving. So the question is: Which part of the circuit or PCB depends on the output current?

Thank you in advance

Huisman
  • 10,594
  • 2
  • 19
  • 40
Nakh0d4
  • 113
  • 1
  • 9
  • 3
    Try using a simulator then introduce capacitance across the L1 inductor to represent its self resonant frequency then add leakage inductance on the secondary and inter-winding capacitance etc.. – Andy aka Jun 05 '19 at 08:59
  • 5
    This is called ringing. Welcome to real life. One easy fix is to slow down the edge rise time with gate resistors... At the cost of efficiency – MadHatter Jun 05 '19 at 12:06
  • 1
    This is usually solved by snubber network across diode or/and transistors. – Chupacabras Jun 22 '22 at 10:12

2 Answers2

1

Just to note, transfer function is irrelevant here. The system is highly nonlinear, and the ringing is asymmetrical. The control loop (if that's what is taken for the TF input) operates at a much lower bandwidth than the ringing here, and its characteristics at frequencies near or above Fsw aren't meaningful.

There is a way in which it could be expressed as a nonlinear transfer function, but this is so complicated as to be useless; the analysis is not taught in undergrad EE for example.

The ringing is most easily explained as the step response of the secondary leakage inductance, with the step being the inverter switching event. Which looks pretty square so this is a pretty accurate description. In the high state, the equivalent circuit is inverter voltage in series with leakage inductance and low-side diode capacitance, and damping can be applied with an R+Cs (Zobel) network across the diode, \$R = \sqrt{\frac{L_L}{C_{JO}}}\$ and \$C_S \geq 2.5 C_{JO}\$. This is true for both phases of inverter output so only one R+C is needed, from the diode-inductor common node to GND.

Note the leakage in this case is between halves of the secondary.

The low-state ringing is harder to explain, as both diodes are turned on by output inductor current. This has to be primary side ringing, manifest on the secondary side through common mode coupling. An R+C on the primary side may help (this time using primary-referred leakage and total MOSFET capacitance Coss). It could also be inverter loop inductance ringing with Coss.

Tim Williams
  • 22,874
  • 1
  • 20
  • 71
0

Might be an old question but I'd want to give an answer.

Your full bridge is missing a leakage inductor in circuit before the primary winding. That will lower the ringing spike

Sumutiu Marius
  • 101
  • 2