8

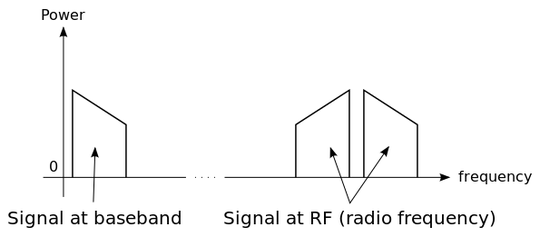
With on-off keying, you have a single carrier wave at a constant frequency transmitting its presence or absence. Now I understand that the crystal will not be perfect so you will have some minimal shift over time in the carrier frequency, but assuming the crystal was perfect you would have zero bandwidth because the frequency doesn't change. But datasheets say that the bandwidth is linked to the data rate somehow, what is that equation and what is using up all that extra spectrum if you don't change the frequency?

Aidan
  • 183
  • 1
  • 7
  • 2
    THe on-off data rate has bandwidth, BW. When the carrier is modulated with this the signal bandwidth BW is transferred by this product to add +/- same BW on the carrier, – Tony Stewart EE75 May 15 '19 at 03:32
  • While a transmitted signal carrying any information has bandwidth, the larger bandwidth is that of the receiver - which must accommodate both the data bandwidth and the relative frequency error of the transmitter. Common cheap regenerative receivers also have a demodulation bandwidth determined by the quenching rate. – Chris Stratton May 15 '19 at 03:42
  • If you attempt to transmit 10Hz 50% duty cycle OOK thru a 1Hz bandwidth, the carrier amplitude will decay only a moderate amount during the OFF time, and the carrier amplitude will increase only a moderate amount during the ON time. You'll need about 5Hz bandwidth to see a large amplitude variation between ON and OFF, because the channel (the filter) has the irksome property of storing energy, and that stored energy causes ISI between a ON and the next OFF, and from that OFF to the next ON. ISI is inter-symbol-interference. – analogsystemsrf May 15 '19 at 03:48
  • Related: [Why is channel capacity a factor of bandwidth instead of frequency?](https://electronics.stackexchange.com/q/86151/6334) – The Photon May 15 '19 at 04:55
  • Also you might want to research the *modulation property* of the Fourier transform. – The Photon May 15 '19 at 05:00
  • @SunnyskyguyEE75 Please don't answer questions in the comment section. – pipe May 15 '19 at 06:35
  • @mkeith Please don't answer questions in the comment section. – pipe May 15 '19 at 06:35
  • @ChrisStratton Please don't answer questions in the comment section. – pipe May 15 '19 at 06:35
  • @analogsystemsrf Please don't answer questions in the comment section. – pipe May 15 '19 at 06:36
  • This is ridiculous. You guys know better but are _still_ in such a hurry to get your opinion out and can't bother to type it up in a format that benefits the site and that can be accepted, voted on, etc. – pipe May 15 '19 at 06:37
  • Imagine OOK where the data rate is, say, 1000 times the carrier frequency. – user253751 May 15 '19 at 09:46
  • Kind-of duplicate: https://electronics.stackexchange.com/questions/272658/why-does-more-bandwidth-guarantee-high-bit-rate – JimmyB May 15 '19 at 10:22
  • 1
    @pipe, I didn't answer the question, really. – user57037 May 15 '19 at 16:11

4 Answers4

11

Only an ideal sine wave with constant amplitude and single frequency that runs for infinitely long in time has extremely narrow bandwidth of a single peak. Having any changes to the ideal sine wave such as changing the amplitude means that since it cannot be represented as a single sine wave any more but a sum of many sine waves of different amplitudes and different frequencies, in frequency domain it means it has a range of frequencies. The faster the changes, the wider the bandwidth.

Justme
  • 127,425
  • 3
  • 97
  • 261
10

On-Off Keying (OOK) is equivalent to AM modulation of the carrier with the data bit-stream with a 100 % modulation index.

As a result the entire spectrum of the bit stream is up-converted to the carrier frequency of the OOK modulator. Additionally, due to AM modulation an image of the data-stream exists below the carrier frequency in addition to the translated spectrum above the carrier.

sstobbe
  • 2,992
  • 1
  • 11
  • 12
4

The bandwidth is not due to carrier frequency drift. As a first approximation, the bandwidth is twice the frequency that modulates the carrier:

enter image description here

This may not be intuitive, but consider that the amplitude modulation (including OOK) is essentially a multiplication of carrier and modulation signals, and basic trigonometry tells us that

$$2 sinA sinB = cos(A - B) - cos(A + B)$$

Dmitry Grigoryev
  • 25,576
  • 5
  • 45
  • 106
2

As sstobbe has pointed out OOK is simply digital AM transmission.

Which mathematically speaking means the Signal is multiplied by the Carrier Frequency to give the Modulated Wave (in the Time Domain).

Convolution theorem states that two signals multiplied together in the time domain is the same as the two signals convolved together in the Frequency Domain.

You can model the Digital signal as a Rectangle function.

Long story short that means that you end up with a shifted form of the below frequency graph, with the center around the carrier frequency.

Plot of sinc(x) function with its frequency spectral components.

Aron
  • 402
  • 2
  • 10