Suppose your sample rate is \$f_s\$
Then, according to Nyquist I can sample signals with a frequency content up to \$f_s/2\$ and use the sampled data to accurately reconstruct my signal.
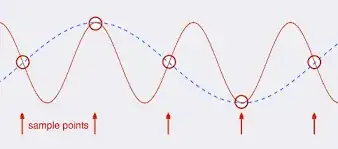
What happens if my signal doesn't "stop" at \$f_s/2\$, then these signals above \$f_s/2\$ will disturb the sampling and my reconstructed signal will not be the same anymore. This effect is called aliasing.
So these signals above \$f_s/2\$ need to be filtered out using an anti-aliasing filter.
However we do not want that filter to affect the signals \$f_s/2\$!
So the filter ideally needs to:
Do nothing when \$f < f_s/2\$
but
block everything when \$f > f_s/2\$
That's impossible to make! So there needs to be a compromise.
When the highest frequency in your signal is close to \$f_s/2\$ then you would need an impossible to make filter to not let it affect your signal frequencies close to \$f_s/2\$
Things become much easier if we either:
Limit the signal frequencies to much smaller frequencies than \$f_s/2\$
or
we increase the sampling frequency so that \$f_s/2\$ ends up at a much higher frequency.
Then we "pull apart" the highest signal frequency and the \$f_s/2\$ frequency.
That then "creates room" for the anti-aliasing filter as the frequency at which the filter should not do anything (highest signal frequency) and the frequency at which everything should be blocked (\$f_s/2\$) will be further apart.