0

In an article by Wie et al. (1989), for the purpose of calculating the gains of a controller, the equations of motion are approximated by the expression for a damped harmonic oscillation:

$$\ddot{\theta} + d \dot{\theta} + \frac{k}{2} \theta = 0$$

where, of course:

$$d = 2 \zeta \omega _n \quad ; \quad \frac{k}{2} = \omega^2 _n$$

In the design example presented in the article, a settling time of $$T_s = 50 \text{ sec}$$ is assumed. Now, the article states that for a critically damped response, $$\omega _n = 0.158 \text{ rad/s.}$$

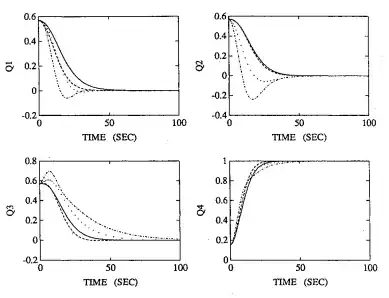
Indeed, using this natural frequency to calculate the controller gains yields responses that settle after about 50 seconds:

enter image description here

However, when using the relation between the settling time and the natural frequency for a critically damped system as presented in this answer, one obtaines:

$$ \omega_n \approx \frac{5.8335}{T_s} = \frac{5.8335}{50} = 0.117 \text{ rad/s.} $$

So the question is, how was the natural frequency calculated in the article?

woeterb
  • 101
  • 2

2 Answers2

1

You need to be careful when using settle time approximations that relate \$\omega_n\$ and \$\zeta\$ to a \$T_s\$.

First, \$T_s\$ is defined as the time where the signal remains within \$\pm x\$% of the final value. Typically the settle limits are \$\pm 2\$% or \$\pm 5\$%, and these limits impact all second order system settle time approximations. Yes, every 2nd order settle time equation is an approximation, and they all differ as a function of \$\zeta\$.

Next, $$\omega_n \approx \frac{5.8335}{T_s},$$ is only a numerical approximation to the normalized unit step response for a critically damped system (i.e., \$\zeta=1\$), which is $$\theta(t)= \left(1-(1+\omega_n t)e^{-\omega_n t}\right)u(t),$$ where \$u(t)\$ is a unit step (aka Heaviside step). The settle time approximation for this is eloquently derived in your "this answer" link using a \$\pm 2\$% window to numerically arrive at \$\omega_n \approx \frac{5.8335}{T_s}\$.

When I look at the graphs of the data you shared, it looks like the 2% settle time for the critically damped trace is closer to 35. This results in \$\omega_n\approx\frac{5.8335}{35}= 0.167\$ rad/sec. A result is closer to the actual \$\omega_n\$ in the article. Better graphs, and clarification on which trace is actually the critically damped one, will improve this estimate.

Sorry, but I do not have free access to your article, so cannot answer your question directly, but most likely the authors knew \$\omega_n\$ directly.

uRog
  • 111
  • 4
  • Thanks @uRog, I am aware that the relation mentioned is merely an approximation. In the article, the authors first define the settling time to be 50 seconds. Next, they calculate \$\omega _n\$, assuming that \$\zeta = 1\$. Yet how remains a mystery. – woeterb May 07 '19 at 13:36
  • Yes, without seeing the paper, it is hard to say. Since you know \$\omega_n\$ and \$\zeta\$, you can use Python + controls package or MATLAB + control toolbox to simulate an initial condition response to replicate Q1. Another option is to plot \$\theta(t)= \left(0.58(1+\omega_n t)e^{-\omega_n t}\right)u(t),\$ vs \$t\$, assuming the i.c. was 0.58, and see what \$T_s\$ really is. This will help you understand what is happening at \$t=50\$ – uRog May 07 '19 at 15:57
  • Already did that, settling times turned out to be much lower than 50. Wondering then why the authors would so explicitly state 50. Regarding access to scientific papers, have you ever heard of Sci-Hub? https://sci-hub.se/ – woeterb May 07 '19 at 16:22
0

I came here looking for an explanation to the same problem in the same article. Just after Equation 34, it is mentioned that:

enter image description here

As the initial eigen angle-to-go in the example is 161.7 deg, they probably assumed it 180 deg and used the modified settling time relation. This leads to a natural frequency value of 0.160 rad/s, which is close to the value of 0.158 rad/s mentioned in the article. I am still trying to figure out a lot of other assumptions used in this article. But hopefully, this will answer your question.

DEBDEEP ROYCHOWDHURY
  • 1
  • 1