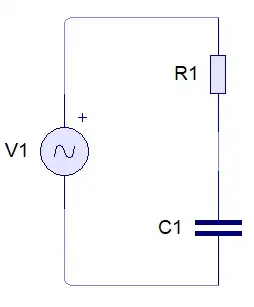
I would like to make it even clearer.
From the circuit above using circuit analysis you'll find the the output voltage in this form below with the time constant \$ \tau = \mathrm{RC} \ \mathrm{seconds}\$. See this for the derivation.
\$
\displaystyle V_{out}(t)= \frac{\mathrm{e}^{-t/\tau}}{\tau} \int V_{in}(t) \: \mathrm{e}^{\: t/\tau} \: \mathrm{d}t
\$
I would also like to generalize the input voltage.
\$
V_{in}(t)= \mathrm{A_0} \mathrm{e}^{\alpha t} \; \sin(\omega t + \phi_0) + \mathrm{DC_{offset}}
\$
Where
- \$\mathrm{A_0}\$ is the amplitude scaling factor
- \$\alpha\$ is the decaying/growth factor (0 = oscillating)
- \$\phi_0\$ is the initial phase offset in radian
- \$\mathrm{DC_{offset}}\$ is the input DC offset in volt
Then
\$
\begin{aligned}
\displaystyle V_{out}(t)&= \frac{\mathrm{e}^{-t/\tau}}{\tau} \int \left[ \mathrm{A_0} \mathrm{e}^{\alpha t} \; \sin(\omega t + \phi_0) + \mathrm{DC_{offset}}\right] \: \mathrm{e}^{\: t/\tau} \: \mathrm{d}t \\
\displaystyle &= \frac{\mathrm{e}^{-t/\tau}}{\tau} \int \left[\mathrm{DC_{offset}}\right] \: \mathrm{e}^{\: t/\tau} \: \mathrm{d}t \quad + \quad \frac{\mathrm{e}^{-t/\tau}}{\tau} \int \left[ \mathrm{A_0} \mathrm{e}^{\alpha t} \; \sin(\omega t + \phi_0)\right] \: \mathrm{e}^{\: t/\tau} \: \mathrm{d}t \\
\displaystyle &= \mathrm{DC_{offset}} + \mathrm{A_0} \frac{\mathrm{e}^{-t/\tau}}{\tau} \int \mathrm{e}^{(\alpha + 1/\tau)t} \; \sin(\omega t + \phi_0) \: \mathrm{d}t\\
\end{aligned}
\$
Solve the integral. You can see the derivation in other SE answer here.
$$\boxed{\int \mathrm{e}^{\mathrm{a}x}\sin( \mathrm{b}x + \phi_0)\;\mathrm{d}x = \frac{\mathrm{e}^{\mathrm{a}x}}{\mathrm{a}^2+\mathrm{b}^2}\left[\mathrm{a}\sin(\mathrm{b}x + \phi_0) - \mathrm{b}\cos(\mathrm{b}x+ \phi_0)\right] + \mathrm{c_1}}$$
I'll further add the initial phase offset constant and angular frequency. It doesn't really matter in the process with this context since they are constants. You can try derive it yourself.
Let's simplify the trigonometric part first. See the derivation of Harmonic Addition Theorem. There's also exist another version with combination from sin, arcsin, arccos, et cetera. Each of it has a certain advantage over another of avoiding signum function, phase adjustment or generalization. I'll only cover the cos arctan version here.
$$\boxed{\gamma\sin(\lambda x+\phi_0)+\delta\cos(\lambda x+\phi_0)= \mathrm{sgn}(\delta) \: \sqrt{\gamma^2+\delta^2} \: \cos(\lambda x + \phi_0 + \phi)}$$
Where
$$\:\phi = \arctan \left( -\:\frac{\gamma}{\delta} \right)\:\mathrm{rad}$$
By substituting it, derationalizing the denominator, and realizing that signum is an odd function, we can simplify the integral further.
\$
\begin{aligned}
\int \mathrm{e}^{\mathrm{a}x}\sin(\mathrm{b}x + \phi_0)\;\mathrm{d}x &= \frac{\mathrm{e}^{\mathrm{a}x}}{\mathrm{a}^2+\mathrm{b}^2}\left[\mathrm{a}\sin(\mathrm{b}x + \phi_0) + (-\mathrm{b})\cos(\mathrm{b}x + \phi_0)\right] + \mathrm{c_1}\\
&= \frac{\mathrm{e}^{\mathrm{a}x}}{\mathrm{a}^2+\mathrm{b}^2}\left[ \mathrm{sgn}(-b)\sqrt{\mathrm{a}^2+\mathrm{(-b)}^2} \: \cos\left(\mathrm{b}x + \phi_0 + \phi \right)\right] + \mathrm{c_1}\\
&=\frac{\mathrm{e}^{\mathrm{a}x}}{\sqrt{\mathrm{a}^2+\mathrm{b}^2}} \: \mathrm{sgn}(-b) \cos\left(\mathrm{b}x+\phi_0 + \phi \right)+ \mathrm{c_1}\\
&=\frac{\mathrm{e}^{\mathrm{a}x}}{\sqrt{\mathrm{a}^2+\mathrm{b}^2}} \: \mathrm{sgn}(-b) \cos\left[\mathrm{b}x+\phi_0 + \arctan\left(-\:\frac{\mathrm{a}}{\mathrm{-b}}\right) \right]+ \mathrm{c_1}\\
&= \frac{-\mathrm{sgn}(b)}{\sqrt{\mathrm{a}^2+\mathrm{b}^2}} \: \mathrm{e}^{\mathrm{a}x} \cos\left[\mathrm{b}x+\phi_0 + \arctan\left(\frac{\mathrm{a}}{\mathrm{b}}\right) \right]+ \mathrm{c_1}
\end{aligned}
\$
Thus we get the integral result in the simplest form
$$\boxed{\int \mathrm{e}^{\mathrm{a}x}\sin( \mathrm{b}x + \phi_0)\;\mathrm{d}x = \frac{-\mathrm{sgn}(b)}{\sqrt{\mathrm{a}^2+\mathrm{b}^2}} \: \mathrm{e}^{\mathrm{a}x} \cos\left[\mathrm{b}x+\phi_0 + \arctan\left(\frac{\mathrm{a}}{\mathrm{b}}\right) \right]+ \mathrm{c_1} }$$
Lets continue our attempt to solve the output voltage
\$
\begin{aligned}
\displaystyle V_{out}(t)&= \mathrm{DC_{offset}} + \mathrm{A_0} \frac{\mathrm{e}^{-t/\tau}}{\tau} \int \mathrm{e}^{(\alpha + 1/\tau)t} \; \sin(\omega t + \phi_0) \: \mathrm{d}t \\
&= \small \mathrm{DC_{offset}} + \mathrm{A_0} \frac{\mathrm{e}^{-t/\tau}}{\tau} \left[ \frac{- \mathrm{sgn}(\omega) }{\sqrt{\mathrm{(\alpha + 1/\tau)}^2+\mathrm{\omega}^2}} \: \mathrm{e}^{\mathrm{(\alpha + 1/\tau)}t} \cos\left[\mathrm{\omega}t+\phi_0 + \arctan\left(\frac{\mathrm{(\alpha + 1/\tau)}}{\mathrm{\omega}}\right) \right] + \mathrm{c_1} \right] \\
&= \small \mathrm{c_1} \mathrm{A_0} \frac{\mathrm{e}^{-t/\tau}}{\tau} + \mathrm{DC_{offset}} + \frac{ - \mathrm{sgn}(\omega) \: (\mathrm{A_0} / \tau)}{\sqrt{\mathrm{(\alpha + 1/\tau)}^2+\mathrm{\omega}^2}} \: \mathrm{e}^{\mathrm{\alpha}t} \cos\left[\mathrm{\omega}t+\phi_0 + \arctan\left(\frac{\mathrm{(\alpha + 1/\tau)}}{\mathrm{\omega}}\right) \right] \\
\end{aligned}
\$
Solve \$\mathrm{c_1}\$ constant by inspecting the capacitor output voltage at specific time, usually the initial at time=zero or initial condition \$V_{out}(0)\$.
\$
\begin{aligned}
\displaystyle V_{out}(t) &= \small \mathrm{c_1} \mathrm{A_0} \frac{\mathrm{e}^{-t/\tau}}{\tau} + \mathrm{DC_{offset}} + \frac{ - \mathrm{sgn}(\omega) \: (\mathrm{A_0} / \tau)}{\sqrt{\mathrm{(\alpha + 1/\tau)}^2+\mathrm{\omega}^2}} \: \mathrm{e}^{\mathrm{\alpha}t} \cos\left[\mathrm{\omega}t+\phi_0 + \arctan\left(\frac{\mathrm{(\alpha + 1/\tau)}}{\mathrm{\omega}}\right) \right] \\
\displaystyle V_{out}(0) &= \small \mathrm{c_1} \mathrm{A_0} \frac{\mathrm{e}^{-(0)/\tau}}{\tau} + \mathrm{DC_{offset}} + \frac{ - \mathrm{sgn}(\omega) \: (\mathrm{A_0} / \tau)}{\sqrt{\mathrm{(\alpha + 1/\tau)}^2+\mathrm{\omega}^2}} \: \mathrm{e}^{\mathrm{\alpha}(0)} \cos\left[\mathrm{\omega}(0)+\phi_0 + \arctan\left(\frac{\mathrm{(\alpha + 1/\tau)}}{\mathrm{\omega}}\right) \right] \\
\displaystyle V_{out}(0) &= \mathrm{c_1} \mathrm{A_0} \frac{1}{\tau} + \mathrm{DC_{offset}} - \frac{ \mathrm{sgn}(\omega) \: (\mathrm{A_0} / \tau)}{\sqrt{\mathrm{(\alpha + 1/\tau)}^2+\mathrm{\omega}^2}} \: \cos\left[\phi_0 + \arctan\left(\frac{\mathrm{(\alpha + 1/\tau)}}{\mathrm{\omega}}\right) \right] \\
\displaystyle \mathrm{c_1} \mathrm{A_0} \frac{1}{\tau} &= V_{out}(0) - \mathrm{DC_{offset}} + \frac{ \mathrm{sgn}(\omega) \: (\mathrm{A_0} / \tau)}{\sqrt{\mathrm{(\alpha + 1/\tau)}^2+\mathrm{\omega}^2}} \: \cos\left[\phi_0 + \arctan\left(\frac{\mathrm{(\alpha + 1/\tau)}}{\mathrm{\omega}}\right) \right]
\end{aligned}
\$
Conclusion
With
$$
V_{in}(t)= \mathrm{A_0} \mathrm{e}^{\alpha t} \; \sin(\omega t + \phi_0) + \mathrm{DC_{offset}}
$$
Considering
$$
V_{out}(t) = V_{outNatural}(t) + V_{outForced}(t)
$$
Therefore
$$
\boxed{
\begin{aligned}
V_{out}(t) &= \left[ V_{out}(0) - \mathrm{DC_{offset}} + \frac{ \mathrm{sgn}(\omega) \: (\mathrm{A_0} / \tau)}{\sqrt{\mathrm{(\alpha + 1/\tau)}^2+\mathrm{\omega}^2}} \: \cos\left[\phi_0 + \arctan\left(\frac{\mathrm{(\alpha + 1/\tau)}}{\mathrm{\omega}}\right) \right] \right] \: \mathrm{e}^{-t/\tau} \\
&+ \mathrm{DC_{offset}} + \frac{ - \mathrm{sgn}(\omega) \: (\mathrm{A_0} / \tau)}{\sqrt{\mathrm{(\alpha + 1/\tau)}^2+\mathrm{\omega}^2}} \: \mathrm{e}^{\mathrm{\alpha}t} \cos\left[\mathrm{\omega}t+\phi_0 + \arctan\left(\frac{\mathrm{(\alpha + 1/\tau)}}{\mathrm{\omega}}\right) \right]
\end{aligned}
}
$$
The \$\mathrm{DC_{offset}}\$ (outside the exponential bracket) is a part of Forced Response. Because when there is no input (sine wave or dc offset) only the initial capacitor voltage affecting the output voltage. Read Difference between natural response and forced response? if you still don't understand. Also, the signum function can be omitted since the angular frequency is always positive. But in case you want to play with negative frequency, this form still hold the integral result above.
There you have it, with this calculation process, in your question the phase offset is the arctan function above. You just need to simplify the integral result further.
Simulation
By using CircuitLab, click "edit the above schematic" below, click simulate, and run Time-Domain simulation. CircuitLab has limited functionality, it can't model capacitor initial voltage.
EXP(alpha*t)*SIN(2*pi*f*t+phi_0*180/PI)+DC_offset
EXP(0*T)*SIN(2*PI*4*T+0*180/PI)+0
simulate this circuit – Schematic created using CircuitLab
By using LTspice, see .asc file in pastebin here.

By using Desmos, see here.
I've already double-checked it with LTspice. Report back if there are something wrong with it.