I tried to solve this using the node method and it yields 0 on Mathematica, which I believe isn't correct. I'm trying to solve I1 first.
simulate this circuit – Schematic created using CircuitLab
These are my equations:
Thanks!
I tried to solve this using the node method and it yields 0 on Mathematica, which I believe isn't correct. I'm trying to solve I1 first.

simulate this circuit – Schematic created using CircuitLab
These are my equations:
Thanks!
I think a problem with your work is that you've defined \$I_1\$ as a tautology. Of course \$2\cdot I_1\$ can be defined the way you wrote it. But it doesn't add any information to the problem. It simply re-states things.
Here's a way to write it:
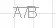
$$\begin{align*} I_1&=\frac{V_1-V_2}{R_1}\\\\ \frac{V_2}{R_1}+\frac{V_2}{R_2}+\frac{V_2}{R_3}&=\frac{V_1}{R_1}+\frac{V_3}{R_2}+\frac{V_4}{R_3}\\\\ \frac{V_3}{R_2}+\frac{V_3}{R_4}+\frac{V_3}{R_5}&=\frac{V_2}{R_2}+\frac{V_4}{R_4}+\frac{V_5}{R_5}\\\\ \frac{V_4}{R_3}+\frac{V_4}{R_4}+2\cdot I_1&=\frac{V_2}{R_3}+\frac{V_3}{R_4}\\\\ \frac{V_5}{R_5}+\frac{V_5}{R_6}&=2\cdot I_1 + \frac{V_3}{R_5}+\frac{0\:\text{V}}{R_6} \end{align*}$$
You should be able to solve for the five unknowns, \$V_2\$, \$V_3\$, \$V_4\$, \$V_5\$, and \$I_1\$ given the knowns (which includes \$V_1\$.)
The solution to your question is illustrated as follows.
The following link is the onlinne calcualtor used to solve the equations: http://math.bd.psu.edu/~jpp4/finitemath/4x4solver.html
If your results differ from those calulated, please indicate where and I will overview it.