Proportional Control Balance Beam

Question

Bit of an unorthodox question I'm sure, but I'm making a balance beam (two rotors on either end of a see saw) with proportional control, and I can't seem to get it to balance at 0.

The proportional gain is controlled via a potentiometer, but there is no 'sweet spot' between oscillation and insufficient motor correction around 0, meaning the beam either oscillates wildly around 0, or the gain is too small and the beam drifts and settles around 5-10 degrees either side. The odd thing is if I set it to go to another angle that isn't 0 it settles no problem.

The values being read from the IMU are fine (it knows it's settling at 5 degrees, it doesn't think it's 0). The sample rate of the IMU matches the update rate of the motors too, so it's not that the I'm feeding the motors old data.

I've tried to take measures to reduce external forces acting on it too, such as the weight of components and turbulence, but to no effect.

I know I can introduce integral control and that will correct against this slight drift, but I'd really like to have this balancing using just proportional - oscillating slightly either side of 0.

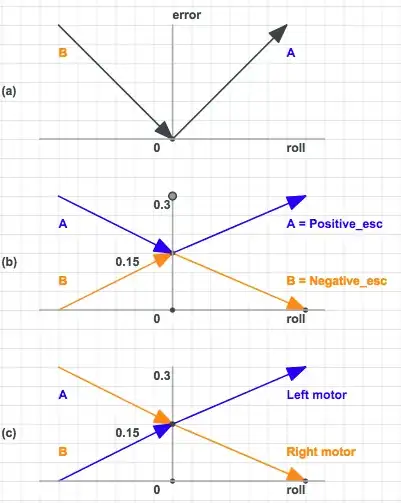
My code is in the format:

float error = sqrt(roll*roll);
Positive_esc = 0.15 + (error*Kp);
Negative_esc = 0.3 - Positive_esc;

if(roll<0){
LeftMotor = Positive_esc;
RightMotor = Negative_esc;
}
if(roll>0){
LeftMotor = Negative_esc;
RightMotor = Positive_esc;
}

Where both motors signals add to make 0.3.

I'm aware there's no definitive answer to this question, but I'm just looking for some creative thinking/some things I might not have considered, because I'm fully stumped on this one.

UPDATE to include transfer functions of response:

UPDATE to include graph of response

As can be seen, the beam will sit quite happily around 3 degrees. However, what concerns me is the positive correction when the error is already positive (can be observed most prominently around t=230).

you gotta turn the GAIN way down, and slow down the system; and accept the final errors. — analogsystemsrf, Mar 22 '19 at 17:32
Inability to maintain a zero, when an offset is easier to maintain, usually indicates the need to introduce an integrator into the control loop. — Chu, Mar 22 '19 at 18:07
some details of your rotor/motors might help us: are they servos?...are they slow?...do they exhibit "stiction"? — glen_geek, Mar 22 '19 at 18:14
Hi. Thanks for the comments on this. I'm aware that a integrator should be introduced into the control loop, and would probably help resolve (or reduce) this issue, but I would like to get the beam oscillating around 0 using just proportional. @Chu are you suggesting this is impossible/very hard to do? — el16a2t, Mar 25 '19 at 15:10
@analogsystemsrf I have turned the gain right down so there isn't sufficient correction to rotate the beam.Then, slowly increasing the gain, to where it's sufficient to correct, it'll either overshoot 0 and be unable to correct back, or, if the gain is turned up slightly more, it'll start crazy oscillations — el16a2t, Mar 25 '19 at 15:15
@glen_geek DC brushless. pretty high rpm so doubt stiction is playing too big a part. (Brushless 1804 2400K if you want to know specifically) — el16a2t, Mar 25 '19 at 15:19
To begin with, why are you mixing `float` and `double`? You should use either and do so consistently. Anyway, motor control is a typical example of where fast PI regulators do well. P not so much. Also, this isn't answerable without you giving an example of the control loop. How does it work, what is the specified resolution and how do you guarantee that it is cyclic? Discussion PID regulators without those parameters isn't very meaningful, as either of them could be the culprit, rather than the math. — Lundin, Mar 26 '19 at 13:50
@Lundin I'm only using floats, should have written it accordingly in the question, apologies. So is it rare to observe a good response when using just P? — el16a2t, Mar 26 '19 at 13:56
@Lundin When referring to resolution what do you mean? I timed my main while loop using a Timer to find my *actual* motor drive update rate. I then set my IMU to read data at the same rate, so old data isn't being sent, and so the motors aren't updating before the next reading. When referring to cyclic what do you mean? It certainly continuously runs and updates - I can observe my IMU data via serial at the expected output rate. — el16a2t, Mar 26 '19 at 14:04
@el16a2t No, you are mixing floats and doubles. `0.15` is a double constant. `sqrt` is a double function. The float equivalents are `0.15f` and `sqrtf`. On systems where single/double precision are different, mixing them might lead to loss of accuracy. So start by fixing the code. And PID regulators can be quite easily written in fixed point, so you don't even need floating point to begin with. Yes it is rare to have a stable P regulator since these are relatively fast-moving things with high response. — Lundin, Mar 26 '19 at 14:05
@el16a2t For any form of regulator to make sense, you must have a certain minimum resolution. For motor control that means a PWM output of a certain amount of bits, and an ADC input with at least as many bits. The regulator can never be better than the weakest link - this includes accuracy of the clock, passive components and indeed the data types used in the software. — Lundin, Mar 26 '19 at 14:07
@el16a2t Cyclic control loops are necessary for a PID regulator to work correctly. This means that you must have hard real time. For every x PWM periods, there need to be y ADC conversions, and the software must update the PWM duty cycle within a hard realtime requirement. If you don't design the system like this, everything just dances and oscillates arbitrary beyond your control, and from there it doesn't matter how you write the software, if there is no real-time constraints. — Lundin, Mar 26 '19 at 14:09
@Lundin very helpful thank you. Is it important for the ADC input to match the PWM output in terms of bits, or simply that it is equal/greater? — el16a2t, Mar 26 '19 at 14:10
@el16a2t You can't get better accuracy than the weakest link, but it is nice to have an ADC with greater accuracy than the output. However, getting 16 or 32 bit PWM resolution is easy - getting up to 16 bit ADC resolution, not so easy. You'd have to use delta sigma ADC that are usually slower than SA ADC. But you probably don't need that high accuracy. 10 bits or so is sufficient for most applications. — Lundin, Mar 26 '19 at 14:12

Transistor · Answer 1 · 2019-03-25T18:35:52.247

schematic

^{simulate this circuit – Schematic created using CircuitLab}

Figure 1. Proportional and "anti-proportional" gain control where both motors sum to unity.

I'm no expert but I would be doing something like this:

// e is the error, Kp is proportional gain
MotorA = 0.5 + Kp * e         // 50% power at zero error
if (MotorA < 0) {MotorA = 0}  // Don't go below 0%
if (MotorA > 1) {MotorA = 1}  // Don't go above 100%
MotorB = 1 - MotorA           // Sum to 100%

At balance the motors will run at 50%.

Update after revised code added:

float error = sqrt(roll*roll);
Positive_esc = 0.15 + (error*Kp);
Negative_esc = 0.3 - Positive_esc;

if(roll<0){
  LeftMotor = Positive_esc;
  RightMotor = Negative_esc;
}
if(roll>0){
  LeftMotor = Negative_esc;
  RightMotor = Positive_esc;
}

This code gives the following transfer functions.

schematic

^{simulate this circuit}

Figure 2. The upgraded code has major issues.

Note that your Positive_esc and Negative_esc are not complimentary. The big problem is the major discontinuity of the left and right motor drives around the zero point.

Did you try my suggested code?

Hi @Transistor. I tried your suggested code, but as it is simply the same as mine (however with a clamp at the minimum and maximum drive limits - very useful and sensible addition, thanks very much) I observed a very similar response. In your diagram (b) is incorrect - Negative_esc will never be greater than 0.15. In fact at 0, both Positive_esc and Negative_esc will be 0.15, so there *is* continuity of both motor drives around the 0 point. I will update the question to include these transfer functions. — el16a2t, Mar 26 '19 at 13:41

score 1 · Answer 2 · edited Mar 23 '19 at 16:27

1

Because

$$ A = \begin{cases} k_p \cdot error & error > 0 \\ \frac{1}{2} - k_p \cdot error & \text{otherwise} \end{cases} $$ and $$ B = \begin{cases} \frac{1}{2} - k_p \cdot error & error > 0 \\ k_p \cdot error & \text{otherwise} \end{cases} $$

In other words, you have honkin' big discontinuities in your motor drives. Even if this would otherwise lead to correct behavior (which I doubt), the motors are going to go crazy close to zero error.

("honkin' big" = American slang for "very big".)

schematic

^{simulate this circuit – Schematic created using CircuitLab}

Figure 1. Graphical representation showing discontinuities. (Added by @Transistor.)

edited Mar 23 '19 at 16:27

Transistor

168,990
12
186
385

answered Mar 22 '19 at 20:08

TimWescott

44,867
1
41
104

@Transistor if I'm reading the OP's code right, B goes negative. I'm not sure that's the intent -- your graph (thank you, but!) would work if they're using the absolute value of \$error\$ when it is negative. – TimWescott Mar 23 '19 at 16:00
Agreed. I've redrawn it, paying much more attention to the equations. B would go in reverse, if possible for a negative error or stop if it's clamped at zero. Does that agree with your equations now. I've never come across your notation style before. Does it have a name? – Transistor Mar 23 '19 at 16:28
@Transistor you mean this: \$\begin{cases} 3 & 0 < x < 4 \\ 0 & \text{otherwise} \end{cases}\$? I'm not absolutely sure what the official name is, but I'm almost certain it's "piecewise". It's pretty common in the technical literature -- you should have run across it even in advanced algebra or calculus. In LaTeX you use the "cases" environment. – TimWescott Mar 23 '19 at 16:57
That's it. It may not have been invented when I was studying. Thanks. – Transistor Mar 23 '19 at 16:59
Sorry for the confusion, caused by me oversimplifying my code for the sake of demonstration. Neither motor signal is ever negative, and 'error' is an absolute value. Essentially both motors sum to x, and if the tilt is one way Motor A = 0.5x + (Kp * error). If the tilt is the other way Motor B = 0.5x + (Kp * error). The other motor in both cases, as @Transistor phrased it, observes 'anti-proportional' gain. In short, the signal of one motor increases proportional to the error and the signal of the other decreases proportional to the error, so that they always sum to 'x'. – el16a2t Mar 25 '19 at 15:30
It's time to fix the question then. – Transistor Mar 25 '19 at 15:33
This will get you my mathematical expression for the behavior, which you can correct to yours: ```$$ A = \begin{cases} k_p \cdot error & error > 0 \\ \frac{1}{2} - k_p \cdot error & \text{otherwise} \end{cases} $$``` – TimWescott Mar 25 '19 at 17:23
@TimWescott I'm a complete amateur at this so unfortunately that just looks like a load of french to me - do you mind elaborating or can you link me to somewhere where I can read more? – el16a2t Mar 26 '19 at 13:52
It looks like you've expanded your question in a way that makes a decent alternative. If you get deep into this stuff, look up LaTeX and Mathjax. – TimWescott Mar 26 '19 at 17:15

Proportional Control Balance Beam

2 Answers2